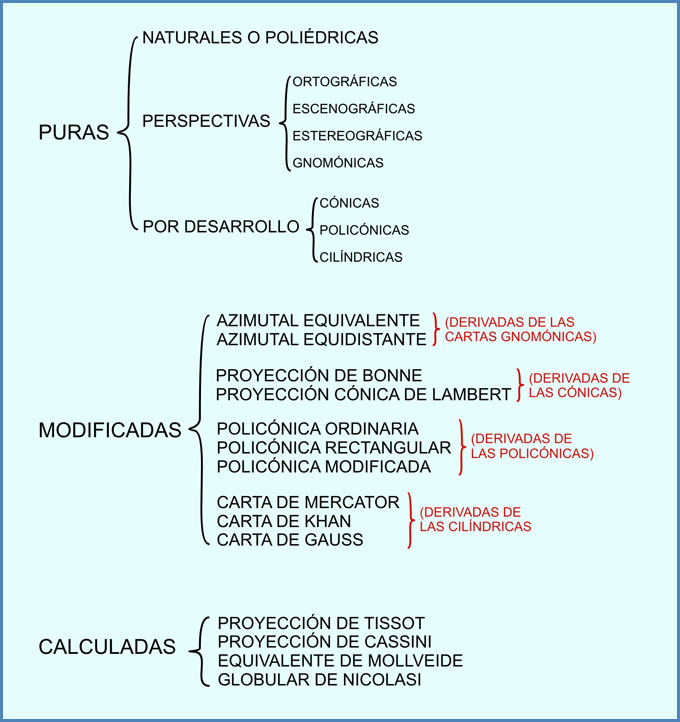
Viene de: Proyecciones Estereográficas y Gnomónicas (clase 9).
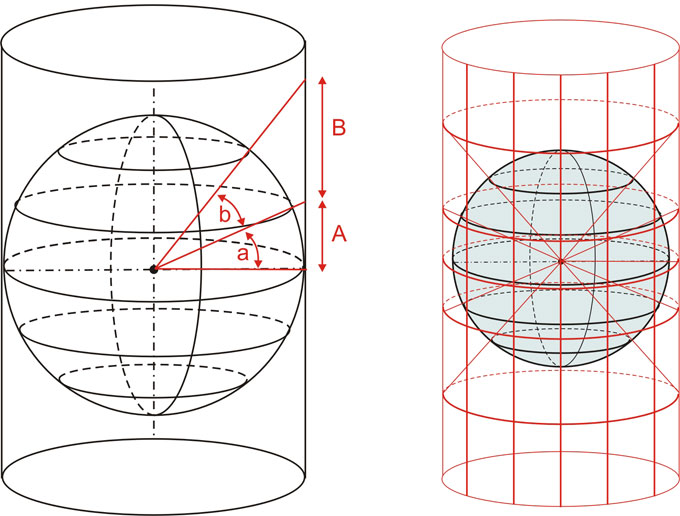
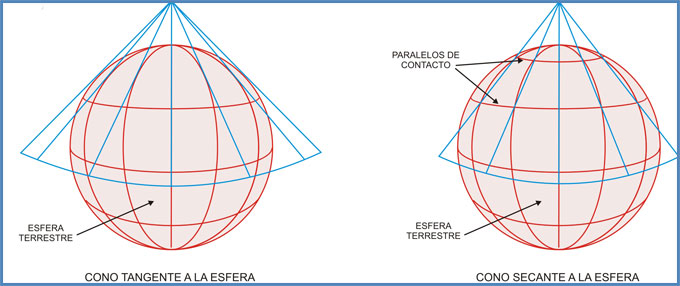
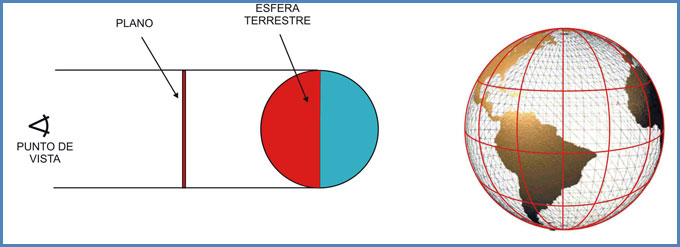
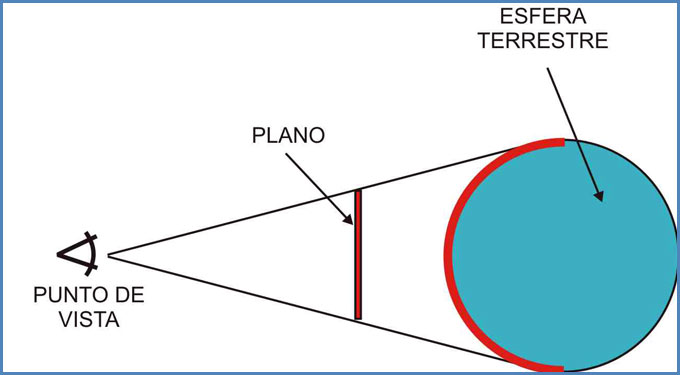
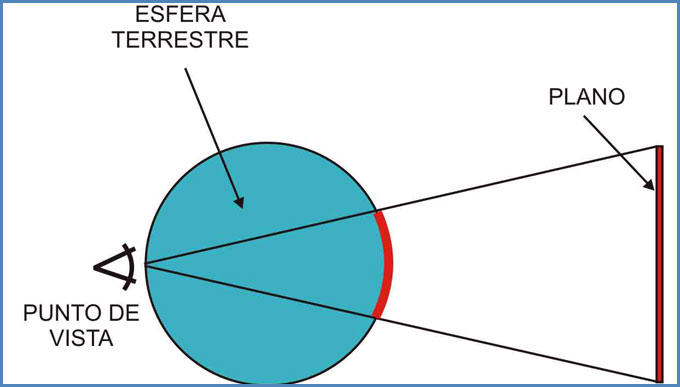
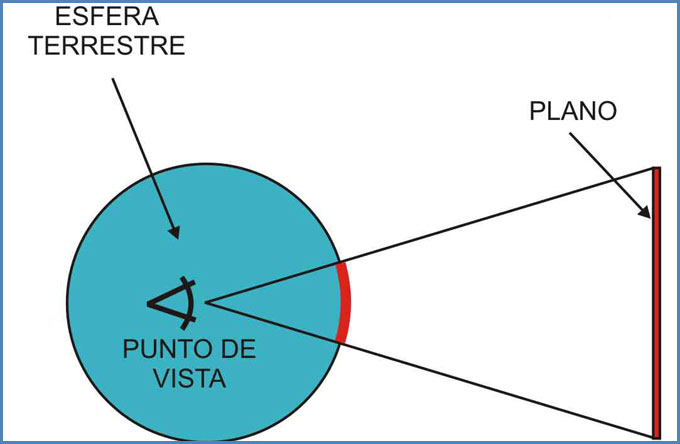
Muchas veces hemos oído decir que la carta Mercator es aquella que surge de proyectar todos los puntos de la esfera terrestre sobre un cilindro, que más tarde se desarrolla a fin de obtener una carta. Esto en realidad es válido solo con fines didácticos, ya que la proyección que surge de proyectar una esfera sobre un cilindro es la llamada cilíndrica pura o cilíndrica centrográfica. En esta última, el eje del cilindro es coincidente con el eje terrestre, siendo dicho cilindro tangente a la Tierra en el Ecuador. El punto de vista en este tipo de proyección se ubica en el centro mismo del globo terráqueo, desde donde se proyectan al cilindro exterior todos los meridianos y paralelos terrestres.

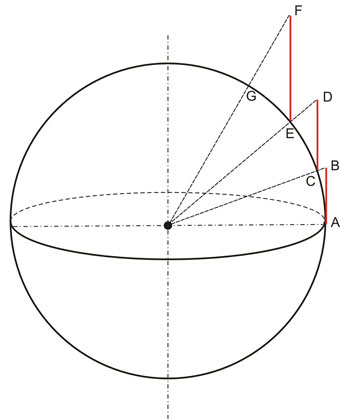
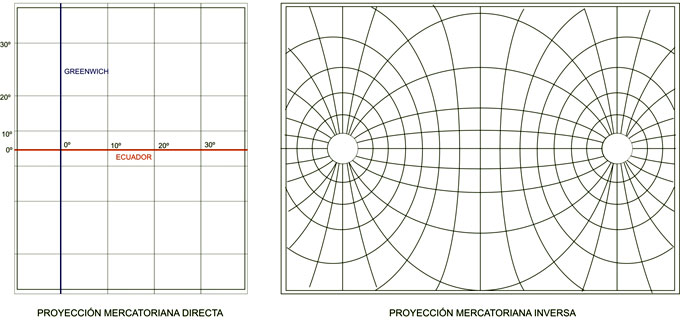
Como se puede apreciar, los meridianos se ven como rectas paralelas equidistantes entre sí y perpendiculares al Ecuador. A su vez, los paralelos resultan rectas paralelas al Ecuador y cuyas distancias a este último están en relación directa con la latitud representada, siendo dichas distancias mayores cuanto mayor sea la latitud a representar. En el gráfico de la figura anterior se ve claramente cómo ángulos iguales (a y b) en la esfera terrestre no representan distancias iguales sobre el cilindro (A y B).
El inconveniente que significan las diferencias en las distancias en una proyección cilíndrica no es, como se cree, el problema principal por el cual dicha forma de representación no puede ser utilizada en navegación. La mayor dificultad reside, a decir verdad, en que dicha proyección no permite conservar los ángulos iguales, es decir: los rumbos.
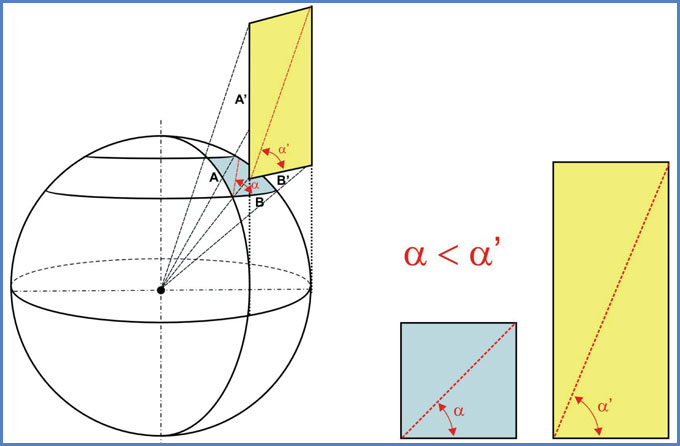
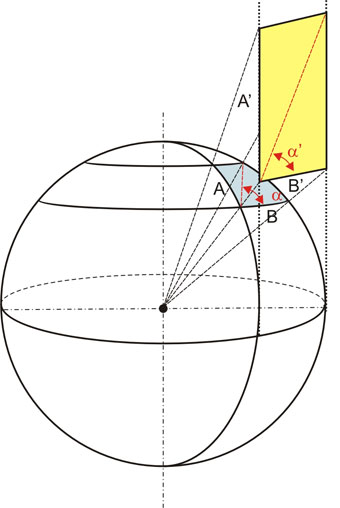
Aquí se ha proyectado el área terrestre cuyos lados son A y B, quedando conformada en el cilindro la figura cuyos lados son A’ y B’. Como puede verse, el área proyectada se ve un tanto deformada, haciéndose más alargada en sentido vertical. Esto es resultado de lo visto anteriormente. Las distancias A y B en la esfera no guardan la misma proporción que las distancias A’ y B’ en el cilindro.
Por ese motivo, si se pretendiese atravesar diagonalmente el área terrestre de la figura (zona celeste), sería necesario hacerlo cumpliendo una derrota con un ángulo a respecto del paralelo del lugar. Esta derrota representada en la carta de papel (zona amarilla) correspondería al ángulo a’. Como se aprecia claramente en la figura anterior, queda claro que, producto del alargamiento de la figura proyectada, el ángulo a’ es mayor que el ángulo a.
Las proyecciones cilíndricas puras, si bien tienen la ventaja de que la loxodrómica queda representada por una recta, no pueden se utilizadas en navegación por no conservar los ángulos iguales. Esto fue resuelto por Gerard Kremer, más conocido como Mercator.
Continua en: Proyecciones Modificadas (clase 11)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfonoCel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!