Viene de: Las distintas proyecciones cartográficas II.
En la entrega anterior habíamos comenzado a desgranar el tema de las proyecciones por desarrollo, entre las que se encuentran las cónicas, las polifónicas y las cilíndricas, siendo estas últimas las que más nos interesan por ser la base de la proyección mercatoriana. Alguna vez a todos nos han enseñado que la carta Mercator es aquella que surge de proyectar todos los puntos de la esfera terrestre sobre un cilindro, que más tarde se desarrolla a fin de obtener una carta. Esto es válido solo con fines didácticos pero en realidad no es correcto. Trataremos de comprender en esta entrega el fundamento principal para la construcción de las cartas Mercator, utilizadas por todos nosotros.
Las Proyecciones Cilíndricas
La proyección cilíndrica, como dijimos anteriormente, surge de proyectar una esfera sobre un cilindro que posteriormente se desarrolla. La representación cilíndrica más típica es la cilíndrica pura o cilíndrica centrográfica. En esta última, el eje del cilindro es coincidente con el eje terrestre, siendo dicho cilindro tangente a la Tierra en el Ecuador. El punto de vista en este tipo de proyección se ubica en el centro mismo del globo terráqueo, desde donde se proyectan al cilindro exterior todos los meridianos y paralelos terrestres.
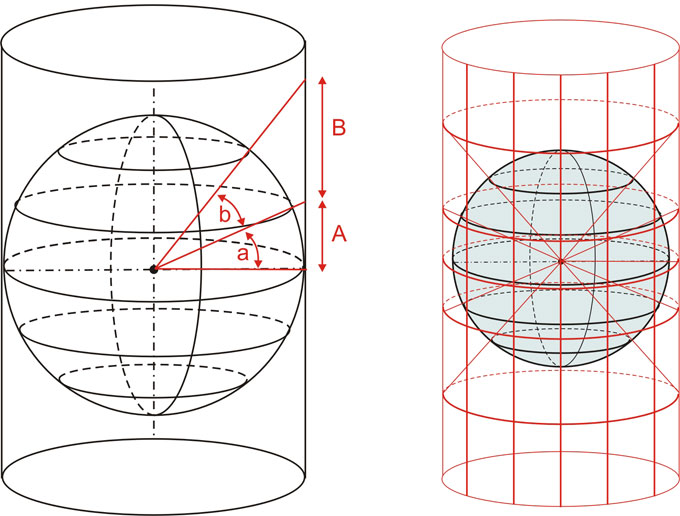
Como se puede apreciar, los meridianos se ven como rectas paralelas equidistantes entre sí, y perpendiculares al Ecuador. A su vez, los paralelos resultan rectas paralelas al Ecuador y cuyas distancias a este último están en relación directa con la latitud representada, siendo dichas distancias mayores cuanto mayor sea la latitud a representar. En el gráfico de la figura anterior se ve claramente cómo ángulos iguales (a y b) en la esfera terrestre no representan distancias iguales sobre el cilindro (A y B).
El inconveniente que significa las diferencias entre latitudes y longitudes en una proyección cilíndrica no es como se cree, el problema principal por el cual dicha forma de representación no puede ser utilizada en navegación. La mayor dificultad reside, a decir verdad, en que dicha proyección no permite conservar los ángulos iguales.
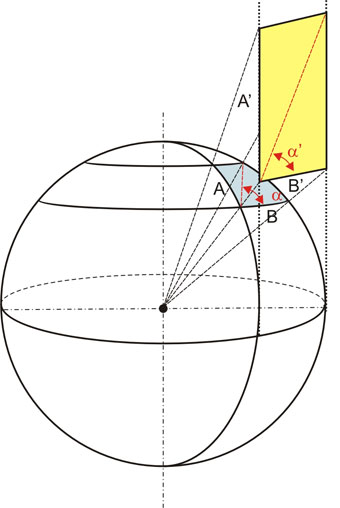
Aquí se ha proyectado el área terrestre cuyos lados son A y B, quedando conformada en el cilindro la figura cuyos lados son A’ y B’. Como puede verse, el área proyectada se ve un tanto deformada, haciéndose más alargada en sentido vertical. Esto es resultado de lo visto anteriormente. Las distancias A y B en la esfera no guardan la misma proporción que las distancias A’ y B’ en el cilindro. Por ese motivo, si se pretendiese atravesar diagonalmente el área terrestre de la figura (zona celeste) sería necesario hacerlo cumpliendo una derrota con un ángulo α. Esta derrota representada en la carta de papel (zona amarilla) correspondería al ángulo α’. Si bien no se aprecia claramente en la figura, queda claro que, producto del alargamiento de la figura proyectada, el ángulo α’ es mayor que el ángulo α.
Las proyecciones cilíndricas puras, si bien tienen la ventaja de que la loxodrómica queda representada por una recta, no pueden se utilizadas en navegación por no conservar los ángulos iguales. Esto fue resuelto por Gerard Kremer, más conocido como Mercator.
Las Proyecciones Modificadas
La mercatoriana es una proyección perteneciente al grupo de las modificadas, y es una derivada de las cilíndricas. El célebre cartógrafo partió de la proyección cilíndrica centrográfica y la modificó sustancialmente. La base principal de dicha modificación se basa en que reemplazó al único cilindro por una serie infinita de ellos, cada uno de los cuales es tangente a lo largo de toda la superficie terrestre. Cada uno de los cilindros de la proyección mercatoriana, una vez desarrollados, solo tienen en cuenta el crecimiento de la escala de las latitudes, mientras que la separación de los meridianos se mantiene constante e idéntica a la correspondiente al cilindro tangente en el Ecuador.
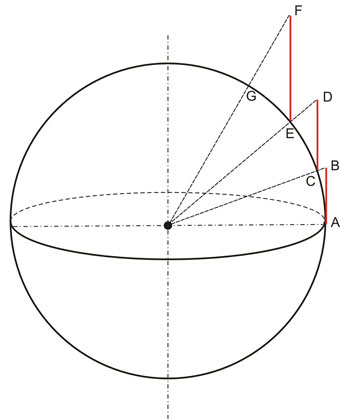
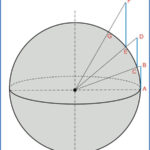
Los triángulos ABC (considerado recto en C), CDE (considerado recto en E) y EFG (considerado recto en G) son el resultado de proyectar, desde el centro de la esfera, los puntos C, E y G sobre distintos cilindros, cada uno de los cuales es tangente a los puntos proyectados. Una vez sumados los distintos trozos de proyección se obtendrá una carta cuya representación gráfica es también conocida como “latitudes aumentadas”.
La fórmula matemática que resultó sería la base de la proyección mercatoriana y se utilizó por primera vez en una carta publicada en Duisburgo en el año 1569. Por ese entonces no se conocía con precisión el radio terrestre, por lo que dicha fórmula era válida solamente para una Tierra esférica. Por esa razón se consideró a dicha proyección dentro del tipo de las esféricas. Esto traía acarreadas algunas imprecisiones, las que fueron resueltas algunos años después, cuando la ciencia permitió conocer con exactitud el radio terrestre en los diferentes puntos de la Tierra. A partir de entonces fue introducido en la fórmula original un factor de corrección, a fin de suprimir los inconvenientes antes mencionados.
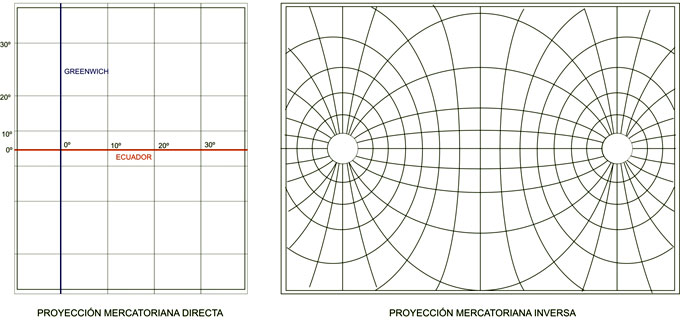
Dependiendo de la posición que ocupe el cilindro que se circunscribe a la esfera terrestre, la proyección resultante recibe diferentes denominaciones. La mercatoriana vista con anterioridad, en la que el cilindro es tangente en el Ecuador, recibe el nombre de proyección mercatoriana directa. Esta es, sin lugar a dudas, la más empleada de todas las proyecciones.
Cuando el cilindro es tangente a cualquier otro círculo máximo, recibe el nombre de transversa. Aquí puede darse el caso de que la tangencia sea con un meridiano cualquiera, proyección que llevará el nombre de mercatoriana inversa; o bien que la tangencia sea con cualquier otro círculo máximo. En este último caso la resultante recibirá el nombre de proyección mercatoriana oblicua. La proyección mercatoriana inversa es útil cuando lo que se desea representar en una zona comprendida entre los polos, sin abarcar demasiada extensión en longitud. Pueden ser utilizadas también en navegaciones cercanas a cualquiera de los polos. En estos casos (latitudes altas) los meridianos presentarán una ligera curvatura, mientras que los paralelos se asemejarán a círculos.
Dentro de las proyecciones modificadas, la otra proyección muy utilizada es la azimutal equidistante, derivada de las proyecciones gnomónicas. Dentro de esta categoría podemos encontrar las tres clases de gnomónicas vistas con anterioridad: polar, meridiana y horizontal, dependiendo de la posición del plano de tangencia.
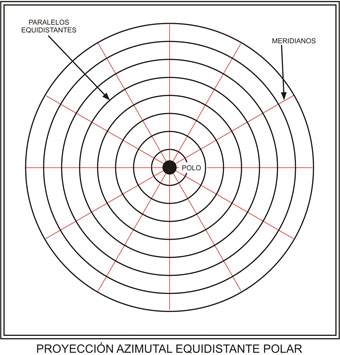
La más común de todas es la carta con proyección azimutal equidistante polar, cuya ventaja fundamental reside en que en una sola carta puede representarse todo el globo terráqueo.
En este tipo de proyección, los meridianos serán rectas concurrentes que convergerán en los polos, mientras que los paralelos serán círculos concéntricos separados, de manera tal de conservar sus distancias reales en la Tierra. De este modo, los círculos que representan a cada uno de los paralelos serán equidistantes entre sí, lo que da origen a la denominación de la proyección. La dificultad de este tipo de proyección es que sufre grandes deformaciones en la cercanía de los polos, tanto en ángulos como en distancia. Esta es en realidad una proyección calculada, ya que no surge geométricamente sino a partir de formulaciones matemáticas.
Este tipo de proyección es utilizada, por ejemplo, en la representación de la esfera celeste que utiliza el identificador de estrellas conocido como “Star Finder Nº 2102”.
Propiedades de las Proyecciones
Como ya hemos visto, en el pasaje de una esfera a un plano se producen inevitablemente errores, ya que es imposible conservar todas las propiedades geométricas de la esfera original. Cuando hablamos de propiedades geométricas nos referimos fundamentalmente a tres de ellas: ángulos, superficies y distancias. De la conservación de estas tres propiedades surge la clasificación siguiente:
- Proyecciones conformes: Se dice que una carta es “conforme” cuando mantiene los ángulos en que se cortan dos líneas cualesquiera sobre la superficie terrestre. Esto sólo es posible siempre y cuando los meridianos y paralelos se corten en ángulo recto y además la escala sea la misma en todas las direcciones, alrededor de un punto cualquiera. La condición de conformidad solo puede mantenerse en pequeñas áreas de una misma representación. Por esa razón, la utilización del rótulo “conforme” es a menudo erróneo en ciertos casos.
- Proyecciones equivalentes: Se dice que un mapa es equivalente cuando la superficie graficada en el plano del papel guarda equivalencia con las superficie terrestre representada. Como es de esperar, no es posible mantener la equivalencia sin deformar los ángulos originales de la esfera. Por tal motivo, si una proyección se considera equivalente, de ningún modo puede ser conforme a la vez.
- Proyecciones equidistantes: Se denomina así a aquellas proyecciones en las cuales se conserva la proporción en las distancias entre la carta y su representación gráfica. Tal es el caso de la proyección azimutal equidistante vista con anterioridad, en la cual los paralelos de la carta eran equidistantes, respetando las distancias entre los paralelos terrestres.
Darío G. Fernández
Director del ISNDF
 Proyecciones Modificadas (Clase 11)
Proyecciones Modificadas (Clase 11)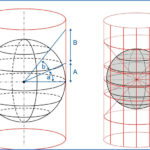 La Proyección Cilíndrica (clase 10)
La Proyección Cilíndrica (clase 10)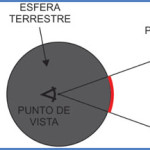 Las distintas proyecciones cartográficas (clase 8)
Las distintas proyecciones cartográficas (clase 8) La longitud en el mar (parte 2)
La longitud en el mar (parte 2) La longitud en el mar (parte 1)
La longitud en el mar (parte 1)