curso de patron de yate | Instituto de Navegación

30/05/2024 by Instituto Superior de Navegación

Cálculo de la Loxodromia (Clase 39)

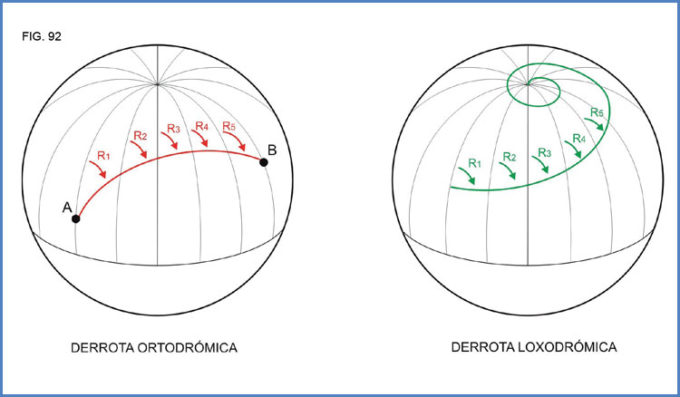
Viene de Conceptos de Ortodromia y Loxodromia (Clase 38)

Como decíamos en el Capítulo V, utilizando una carta Mercator de una zona poco extensa, la determinación de la distancia a navegar puede resolverse fácilmente por el método gráfico. Esto es: uniendo los puntos de salida y de llegada con una línea y trasladando su medida con un compás de punta seca a la escala de las latitudes. Para la determinación del rumbo la cosa es aún más sencilla y puede hacerse utilizando el talco o las reglas paralelas.
Ahora bien, si lo que se pretende es determinar el rumbo y la distancia loxodrómica a navegar entre dos puntos lejanos, esto ya no puede resolverse gráficamente, dado que la carta necesaria debería representar una zona muy extensa y el resultado obtenido padecería de imprecisiones importantes. En tal caso, lo conveniente es recurrir a la trigonometría a través de formulaciones matemáticas sumamente sencillas. Por otra parte, es posible también arribar al mismo resultado mediante el uso de tablas que resuelven las fórmulas matemáticas antes mencionadas. Estas tablas se conocen como “Tablas de Estima”. Analizaremos el tema en la representación de la figura No 93: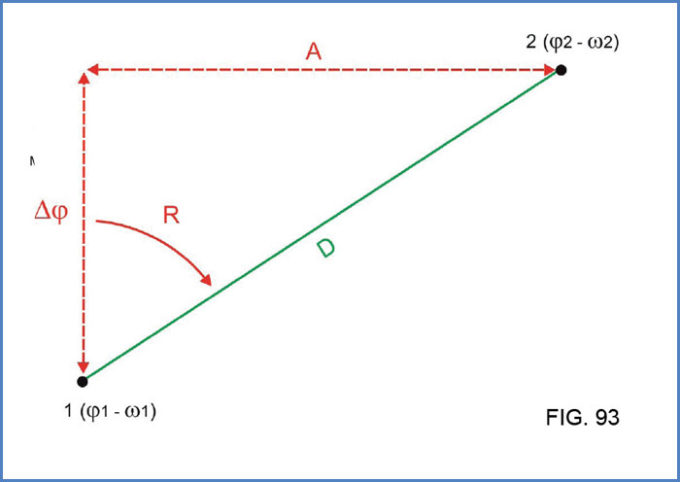

Supongamos que se desea navegar desde el punto 1, cuyas coordenadas son j1 (latitud) y w1 (longitud), hacia el punto 2, con coordenadas j2 y w2. Como puede apreciarse, queda conformado un triángulo rectángulo con los siguientes elementos:

• El ángulo “R” es el rumbo verdadero a seguir.
• “D” es la distancia que separa ambos puntos.
• “Dj” es la distancia recorrida por la embarcación en sentido Norte-Sur. Dado que la escala de distancias expresada en millas náuticas es equivalente a la escala de las latitudes (1 milla náutica = 1’ latitud), podemos decir que “Dj” es la diferencia en latitud entre el punto de salida (1) y el de llegada (2).
• “A” es el apartamiento entre ambos puntos, o lo que es igual a decir que es la distancia recorrida en sentido Este-Oeste. En este caso, el valor del “apartamiento” no es igual a la diferencia en longitud (Dw), dado que ambas escalas no guardan proporcionalidad.
Como sabemos, producto de la proyección cilíndrica, 1o de latitud es igual a 1o de longitud sólo en el Ecuador, tema ya abordado en el Capítulo II. A medida que se navega en latitudes superiores, ambas escalas guardan una relación que, aunque no es exacta, podría expresarse como:
Dw = A / cos jm O bien:
A = Dw x cos jm
Donde jm es la latitud media de la zona. Para obtener jm debe procederse promediando las latitudes de llegada y de salida. En el caso planteado en el esquema anterior, la latitud media se calculará de la siguiente manera:
jm = (j1 + j2) / 2

La fórmula ”Dw = A / cos jm“ expresa simplemente la relación que guardan la escala de las longitudes y la de las latitudes, en función de la latitud media de la zona. Como decíamos anteriormente, dicha fórmula no es exacta por varias razones. La primera es que la misma representa las proporcionalidades que tendrían ambas escalas en una proyección cilíndrica pura para una Tierra esférica, mientras que las cartas que utilizamos a diario se construyen en base a proyecciones cilíndricas modificadas, como son las mercatorianas. Estas últimas incluyen los factores de corrección para el elipsoide. El otro motivo por el cual la expresión anterior no resulta exacta, se debe al hecho de utilizar a la latitud media para establecer las diferencias entre las escalas de latitud y longitud. Esta distorsión, si bien es despreciable en cartas con poca variación de latitud, comienza a ser considerable cuando las cartas utilizadas contienen grandes extensiones, y las variaciones entre la latitud máxima y la mínima son amplias.

A los efectos de subsanar estas inexactitudes existen tablas que permiten su corrección, tal es el caso de una tabla llamada “(1) CORRECCIÓN ADITIVA A LA LATITUD MEDIA jm PARA HACER EXACTA LA FÓRMULA A = Dw x cos jm“.
En realidad, y a los efectos de los cálculos náuticos empleados de manera corriente, dicha corrección no es necesaria y la fórmula anterior resulta perfectamente válida.
Ahora bien, del triángulo rectángulo conformado en la figura No 93, aplicando la trigonometría plana, pueden extraerse algunas fórmulas matemáticas que serán de suma utilidad para resolver la estima de manera sencilla:

1. Dj = D x cos R 2. A = D x sen R 3. tg R = A / Dj
Las fórmulas aquí expresadas y sus variantes, permiten determinar muy fácilmente la nueva posición que tendrá una embarcación a partir de la distancia recorrida y del rumbo navegado. También permiten resolver el problema inverso. Es decir: dadas las coordenadas de salida y de llegada, calcular la distancia que separa ambos puntos y el rumbo al que se deberá navegar.
Para el primer caso (estima directa), aplicando las fórmulas 1 y 2 y teniendo los datos del rumbo (R) y de la distancia (D), se calculan los valores de Dj y apartamiento. A partir de este último, se calcula el valor de Dw utilizando como dato la latitud media a través de la fórmula “Dw = A / cos jm”. Una vez obtenidos dichos valores, se determinan las nuevas coordenadas que tendría la embarcación, simplemente sumándolos o restándolos a las coordenadas del punto de partida. Para la segunda opción (estima inversa), con las coordenadas de salida y de llegada se obtienen en primer lugar los valores de Dj y Dw y se convierte este último dato en apartamiento (A = Dw x cos jm). Habiendo calculado ya este último y con el dato obtenido del Dj, se puede determinar el rumbo a navegar aplicando la fórmula 3 (tg R = A / Dj). Hecho esto, solo resta reemplazar el valor del rumbo en cualquiera de las fórmulas 1 ó 2 y determinar así la distancia a recorrer.
Para clarificar un tanto las cosas, veremos un ejemplo de cada caso:

Ejercicio estima directa:
• Habiendo zarpado desde j1= 32o 44,6’ S y w1= 32o 17,6’ E, y luego de haber recorrido una distancia de 282 millas náuticas a rumbo verdadero 68o. ¿Cuáles serán las coordenadas del punto de llegada?
Calculamos en primer lugar Dj (para no complicar el cálculo en adelante redondearemos las fracciones de minuto a un solo dígito):
Dj = D x cos R Dj = 282’ x cos 68o Dj = 282’ x 0,374606 Dj = 105,6388’ = 1o 45,6’
Continuamos averiguando el apartamiento:
A = D x sen R A = 282’ x sen 68o A = 282’ x 0,927183 A = 261,4656’ = 4o 21,4’
Lo que sigue es convertir el apartamiento en Dw:
Dw = A / cos jm Dw = 4o 21,4’ / cos 33o (redondeamos
a 33o la latitud media)
Dw = 4o 21,4’ / 0,838670 Dw = 5o 11,7’
Habiendo obtenido los valores de Dj y de Dw, lo que resta es sumarlos o restarlos a los valores de las coordenadas de salida según corresponda:

j2 = j1 – Dj (nos encontramos en latitud sur y navegamos con componente norte, por lo tanto deberemos restar la diferencia de latitud)
j2 = 32o 44,6’ – 1o 45,6’
j2 = 30o 59,0’ S Hemos obtenido la latitud del punto de
arribo, haremos lo propio con la longitud:
w2 = w1 + Dw (nos encontramos en longitud este y navegamos con componente este, por lo tanto deberemos sumar la diferencia de longitud)
w2 = 32o 17,6’ + 5o 11,7’
w2 = 37o 29,3’ E
De este modo se han obtenido las coordenadas del punto de llegada a partir de la estima analítica por el método directo. Para concluir el tema, presentaremos un ejercicio por el método inverso.
Ejercicio estima inversa:
• Determinar el rumbo verdadero que se deberá seguir y la distancia a recorrer para navegar desde el puerto de Montevideo, cuyas coordenadas aproximadas son j = 34o 54,5’ S y w = 56o 7,6’ W, hasta Ciudad del Cabo, con coordenadas j = 33o 20,3’ S y w = 18o 25,6’ E.
En primer lugar determinaremos la diferencia en latitud Dj:
Dj = j1 – j2 Dj = 34o 54,5’ – 33o 20,3’

Dj = 1o 34,2’
El segundo paso será determinar el apartamiento, para lo cual será necesario obtener primero el valor de la diferencia en longitud Dw. Téngase en cuenta que en este caso deberán sumarse, ya que una posición se encuentra al Oeste y la otra al Este de Greenwich:
Dw = w1 + w2 Dw = 56o 7,6’ + 18o 25,6’ Dw = 74o 33,2’
El paso siguiente es, a partir de la latitud media de la zona (jm), calcular el valor del apartamiento. En este caso, y dado que la diferencia en latitud es muy poca, utilizaremos un valor de jm de 34o, interpolando aproximadamente. Aplicando la fórmula:
A = Dw x cos jm A = 74o 33,2’ x cos 34o A = 61o 48, 4’ = 3.708,4 Mn
El resultado del apartamiento obtenido en el paso anterior está expresando simplemente que una latitud media de 34o, 74o 33,2’ en la escala de las longitudes equivale en distancia a 61o 48,4’ en la escala de las latitudes, o lo que es lo mismo: 3.708,4 millas náuticas.
Para averiguar el rumbo a seguir aplicaremos la fórmula de la tangente:
tg R = A / Dj
tg R = 61o 48, 4’ / 1o 34,2’ tg R = 39o 22’

Continua en: Tablas de Estima: El problema directo (Clase 40)

Darío G. Fernández
Director del ISNDF

Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!

30/05/2024 by Instituto Superior de Navegación

Conceptos de Ortodromia y Loxodromia (Clase 38)

Viene de La Deriva (Clase 37)

Uno de los temas abordados con menor profundidad, tanto por las escuelas de navegación como por los textos náuticos, es el de la navegación ortodrómica. Esto se debe, probablemente, a que la mayoría de los navegantes deportivos que cruzan el océano suelen hacerlo a vela, decidiendo su travesía en función de los vientos y las corrientes más favorables. En tales casos, el hecho de recorrer una derrota más extensa probablemente no sea de vital importancia. Esto cambia de forma radical cuando se emprenden travesías prolongadas en embarcaciones a motor, donde la dirección de los vientos pierde relevancia en comparación con el ahorro de combustible. Y es ahí donde el concepto de navegar por el círculo máximo se torna de suma importancia, debido a las enormes distancias que pueden acortarse llevando el barco por la ruta correcta.

Ortodromia y Loxodromia

Sabemos que la distancia más corta entre dos puntos que se hallan ubicados sobre una superficie plana es la recta que une ambos puntos. Sobre la superficie terrestre, que es en realidad una esfera, esto podría considerarse válido solo para distancias relativamente cortas. Si, en cambio, se deben unir dos puntos que se encuentran ubicados sobre una esfera y que mantienen una separación importante entre sí, la distancia más corta entre ambos será el arco de círculo máximo que contiene a dichos puntos.

Podríamos definir al círculo máximo como al círculo resultante de intersectar a una esfera con un plano que contenga al centro de la misma. Hablando particularmente de la esfera terrestre, son círculos máximos los meridianos y el Ecuador pero no así los paralelos. Estos últimos son círculos menores, paralelos al Ecuador, pero que no contienen al centro de dicha esfera.

En el esquema de la figura No 90 se han representado los puntos “A” y “B” sobre la superficie terrestre. Aunque a priori puede pensarse que la distancia más corta entre ambos puntos es la línea que los une recorriendo su paralelo (representada en color verde), esto es absolutamente falso. La distancia mínima entre ambos corresponde al arco (representado en color rojo) perteneciente al círculo máximo, que contiene a los puntos en cuestión y que a su vez pasa por el centro de la esfera. Esta última línea recibe el nombre de “derrota ortodrómica” o simplemente “ortodromia”, mientras que a la primera se la denomina “loxodromia”.

En realidad podemos definir a la loxodromia como aquella línea sobre la que navega un buque manteniendo su rumbo constante.

Debido a que la derrota loxodrómica corta a todos los meridianos con igual ángulo, ésta puede ser representada como una línea recta en una carta de proyección Mercator (Fig. 91). La derrota loxodrómica, aunque no es la distancia menor entre dos puntos de la esfera, es siempre preferible a la ortodrómica para distancias no demasiado extensas, debido a la sencillez del procedimiento de navegar a rumbo constante. La derrota ortodrómica, si bien representa a la distancia más corta, tiene la desventaja de que su rumbo no es regular, es decir que el ángulo con el que corta los meridianos va variando, por lo que no puede ser representada como una línea recta en una carta mercatoriana. En dichas cartas, la ortodromia queda representada por una curva con su concavidad hacia el Ecuador y su convexidad hacia los polos. La derrota ortodrómica se verá como una línea recta solo en las cartas de tipo gnomónicas ya que en éstas, y dado que el punto de vista se encuentra en el centro de la esfera, todos los círculos máximos también son rectas. En las cartas con proyección gnomónica, las loxodromias se verán como curvas con su concavidad hacia los polos debido a que siguen la curvatura de los paralelos.

En la figura No 92 puede verse claramente cómo en una ortodromia el rumbo va variando (en este caso aumentando) a medida que atraviesa los diferentes meridianos (R5 > R4 … > R1), mientras que en la loxodromia se mantiene el rumbo constante (R1 = R2 = … = R5). En este último caso puede comprobarse que navegando a rumbo permanente sobre la esfera terrestre, la derrota resultante sería la de una curva que se aproxima cada vez más a alguno de los polos, conformando un recorrido espiralado.

Cuando se navega con cartas con proyección Mercator de zonas reducidas está claro entonces que la manera conveniente de navegar será por la Loxodromia; pero en el caso de navegaciones más extensas será conveniente definir cuál será la derrota más apropiada a seguir. Para ello será necesario hacer un análisis acerca de si la distancia a recorrer sobre la ortodromia es suficientemente menor que sobre la loxodromia, como para justificar así la utilización de la primera. En tal caso, el método a seguir será el de calcular ambas distancias, tanto la loxodrómica como la ortodrómica, y efectuar luego la comparación entre ambas. A continuación, desarrollare-mos en profundidad ambos métodos.

Continua en: Cálculo de la Loxodromia (Clase 39)

Darío G. Fernández
Director del ISNDF

30/05/2024 by Instituto Superior de Navegación

El Abatimiento (Clase 36)

Viene de Estima Directa y Estima Inversa (Clase 35)

Como ya mencionáramos, el viento actúa sobre la embarcación desplazándola en forma lateral. De más está decir que este efecto dependerá de la intensidad del viento reinante, así como también del ángulo con el que incide sobre la embarcación, siendo nulo si el mismo fuese de popa, y máximo cuando se recibe por alguna de las amuras.

Hay que decir además que, si bien es más notorio en embarcaciones de vela, los barcos de motor de importantes francobordos también lo sufren, sobre todo cuando navegan a bajas velocidades.

Como consecuencia del abatimiento, el barco, en lugar de avanzar en la dirección de la línea de crujía (rumbo verdadero de la proa), lo hará en otro sentido, afectado por dicho abatimiento. De no mediar corrientes en la zona, que generen deriva, este nuevo rumbo (el real) recibirá el nombre de derrota verdadera (Dv), mientras que el ángulo formado por el rumbo verdadero de la proa (Rc + Dc + dm) y la derrota verdadera será el abatimiento (a). Fig. 82.

Como puede apreciarse en el esquema de la figura 82, el abatimiento será positivo si es a estribor (ya que habrá que sumarlo al rumbo para obtener la derrota) y negativo si es a babor (caso inverso).

Es sumamente dificultosa la tarea de determinar con precisión la magnitud del abatimiento, sobre todo en embarcaciones de placer. Como dijimos anteriormente, el abatimiento será mayor cuanto mayor sea la superficie que la embarcación presente a la acción del viento. Dado que dicho abatimiento es el desplazamiento lateral que sufre el barco sobre la “superficie” del agua, el ángulo que lo representa estará dado por el que forma la crujía del barco respecto de su “estela” (Fig. 83). Una manera práctica de medirlo, aunque no del todo precisa, es arrojar por la popa el cabo naranja flotante que se utiliza para el salvavidas circular, y medir visualmente el ángulo entre este y la línea de crujía. Por supuesto que esta comprobación esta expuesta a errores, dependiendo su precisión del buen ojo del marino y del conocimiento que este tenga de su propio barco.

Ejemplo:

• ¿Cuál será la derrota verdadera de un barco que navega con un rumbo de compás de 180° y un desvío del mismo de – 6°, si navega en una zona donde la declición magnética es de 8° W? Se tiene en cuenta que el abatimiento sufrido por la embarcación se estima en 10° a estribor.

Dv = Rc + Dc + dm + a Dv = 180° + (- 6°) + (-8°) + 10° Dv = 180° – 6° – 8° + 10° Dv = 176°

En este ejemplo se calculó la derrota verdadera que sigue un barco si navega a un rumbo de compás determinado (estima directa). Es el caso característico en el que un barco de vela no puede seguir una derrota ideal porque el viento no favorece su navegación. En este caso, el capitán tratará de ceñir al máximo para aproximarse a su destino lo más que pueda, para luego determinar su derrota verdadera sobre la carta. La otra opción se daría en caso de que la embarcación sí pueda navegar sobre la derrota ideal, ya sea porque tiene vientos favorables o simplemente porque se trata de un barco a motor. En este caso se calculará el rumbo de compás al que se debe navegar en función de la derrota verdadera deseada (estima inversa). En ambos procedimientos se aplicará la misma fórmula, despejando en cada caso la incógnita a averiguar.

Ejemplo:

• Se pretende calcular el rumbo de compás al que se debe gobernar una embarcación si se desea navegar sobre una derrota verdadera de 240°, teniendo en cuenta que la declinación magnética de la zona es de 6° E, el compás tiene un desvío para ese rumbo de – 3° y el abatimiento sufrido es de 15° a babor.

Dv = Rc + Dc + dm + a Rc = Dv – Dc – dm – a Rc = 240° – (-3°) – (+6°) – (-15°) Rc = 240° + 3° – 6° + 15° Rc = 252°

En definitiva, podemos decir que el abatimiento puede tomarse sencillamente como una corrección adicional que debe hacerse sobre el rumbo del compás, al igual que la declinación magnética y el desvío.

La derrota verdadera hasta aquí calculada solo es válida en caso de navegar en un espejo de agua o en momentos donde no hay corrientes de marea que alteren el rumbo de la embarcación. En caso de existir, dicha corriente afectará en forma decisiva al rumbo, y esto es lo que veremos a continuación.

Continua en: La Deriva (Clase 37)

Darío G. Fernández
Director del ISNDF

30/05/2024 by Instituto Superior de Navegación

Estima Directa y Estima Inversa (Clase 35)

Viene de El reloj de Bitácora y la conservación del tiempo (Clase 34)

Como ya vimos en el Capítulo I, la navegación por estima consiste simplemente en esto: Desde un punto conocido, se navega a un rumbo determinado durante un período de tiempo y a una velocidad establecida hasta la nueva posición. Aquí se fijará un nuevo punto “estimado” (cuya simbología es un punto rodeado de un triángulo) teniendo en cuenta para ello la dirección y distancia recorrida.

Se define como “posición estimada” porque no hay certeza de su exactitud. Cuando por otros métodos (que veremos más adelante) se obtiene una posición cierta o FIX (del inglés “fixing position”), se colocará un círculo alrededor del punto, señalando que lo que se obtuvo es una posición exacta.

Veamos cómo se hace en forma práctica (Fig. 79):

1) Ubicamos en la carta el punto de partida “A”, cuyas coordenadas conocemos.

2) Con los datos del rumbo compás al que venimos navegando, la declinación magnética del lugar y el desvío del compás, obtenemos el rumbo verdadero (Rv) y lo trazamos en la carta con los elementos de dibujo (escuadras, reglas paralelas, etc.).

3) Con el dato de la velocidad que indica la corredera y el tiempo que navegamos desde el punto “A”, podemos calcular la distancia recorrida. Con el compás de punta seca y utilizando la escala de las latitudes, medimos esa distancia y la trasladamos a la recta antes trazada.

4) En este punto colocaremos nuestro punto de estima.

Este procedimiento se conoce como “Estima Directa”.

Cuando se coloca un punto de estima, es conveniente colocar además la hora y los datos de sondaje y corredera.

Ejemplo:

Zarpamos del punto “A”, Lat: 33o 26,600’ S y Long: 50o 48,000’ W a las 11:00 hs, con un rumbo de compás de 75o. A las 12:10 hs, y luego de haber navegado a una velocidad de corredera de 3 Nds, colocamos nuestro nuevo punto de estima teniendo en cuenta que la “dm” de la zona es de 10o W y nuestro compás posee un desvío, al rumbo establecido, de +5o.

Calcularemos entonces el Rv:

Rv = Rc + Dc + dm Rv = 75o + (-10o) + (+5o) Rv = 70o

Calculamos ahora la distancia recorrida:

D = VxT D = 3 Nd x 1h 10 m

En este punto podemos hacer dos cosas: o pasamos 1 h 10 m a hora y fracción de hora (1 h 10 m = 1,1666 hora), o bien pasamos todo a minutos (1 h 10 m = 70 minutos).

Sabemos que la unidad nudo equivale a milla náutica / hora, por lo tanto:

D = 3 Mn/h x 1,1666 h Las unidades “hora” se simplifican, en-

tonces:

D = 3,5 Mn

También se podría hacer lo propio utilizando el tiempo expresado en minutos, para lo cual la unidad de velocidad debería quedar expresada en milla náutica / 60 minutos.

D = 3 Mn/60 m x 70 m D = 3,5 Mn

Hemos arribado al mismo resultado.

Situaremos entonces el punto “A” en la carta y luego, con los datos de “Rv” y “D”, hallaremos nuestra nueva posición de estima (Fig. 80):

Hemos calculado en este caso la posición a la que arribamos a partir del rumbo de compás y la distancia recorrida. A este proceso se lo conoce como “estima directa”. pero podría darse el caso inverso: trazar el rumbo entre dos puntos que deseo unir en la carta, obtener el “Rv”, y a partir de aquí calcular el rumbo de compás al que se debe gobernar. Este será el caso de la Estima Inversa.

Veamos un ejemplo:

• Planificamos cumplir una travesía zarpando a hora bitácora 12:15 hs. desde el punto “A”, Lat: 34o 28,800’ S y Long: 58o 50,600’ W, hasta arribar al punto “B”, Lat: 34o 30,000’ S y Long: 58o 47,400o W. Si navegamos a una velocidad de corredera de 4,9 Nd, la declinación magnética de la zona es de 6o W y el desvío de compás al rumbo establecido es de +3o. ¿A qué rumbo de compás deberé navegar para cumplir con la derrota? ¿A qué hora arribaré al punto “B”?

Para comenzar, grafico ambos puntos en la carta y los uno con una línea (Fig. 81). Con ayuda de las reglas paralelas o el talco, mido el rumbo verdadero al que deberé navegar: en este caso 113o.

Con el dato obtenido, más la declinación magnética y el desvío del compás, aplico la fórmula:

Rv = Rc + Dc + dm Despejo de la formula el “Rc”, que es lo

que deseo averiguar:

Rc = Rv – Dc – dm Rc = 113o – (+3o) – (-6o)

Hemos obtenido el rumbo de compás a gobernar para unir ambos puntos.

Para el cálculo de la hora de arribo, en primer término debo determinar la distancia entre “A” y “B”. Para ello, simplemente traslado la distancia entre ambos puntos (midiéndola con el compás de punta seca) a la escala de las latitudes. El valor en minutos obtenido es la distancia en millas náuticas entre “A” y “B”, en este caso 3,2 Mn.

Para calcular la hora de arribo, vuelvo a aplicar la fórmula de la distancia, teniendo como datos a esta última (3,2 Mn) y a la velocidad (4,9 Nd):

D = V x T

Despejo “T” en la fórmula, puesto que es la incógnita a resolver:

T= D /V T = (3,2 Mn) / (4,9 Mn/h)

Las unidades milla náutica se simplifican entre sí, quedando el resultado expresado en horas:

T = 0,653 h

Para pasar el resultado a horas y minutos (sistema sexagesimal), simplemente multiplico la fracción de horas por 60:

0,653 x 60 m = 39 minutos

Para saber la hora a que se arribará al punto “B”, solo resta sumar el valor “T” (tiempo de navegación) a la hora de zarpada:

Hora de arribo = Hora de zarpada + Tiempo de Navegación

Horadearribo=12h15m+39m Hora de arribo = 12 h 54 m.

En adelante, a la hora de zarpada la llamaremos “Hb1” (hora de bitácora 1), mientras que la hora de arribo será “Hb2” (hora de bitácora 2).

La navegación por estima continúa del mismo modo hasta tanto se pueda obtener un punto cierto o punto “FIX”, momento en el que se corregirá y se continuará la navegación desde ese nuevo punto.

Como ya mencionáramos en el Capítulo 1, el punto FIX puede obtenerse por GPS (navegador satelital), a partir de puntos notables de la costa cuando nos aproximamos a ella (navegación costera), o bien por cálculo astronómico cuando no se tienen referencias de la costa.

Todos los cálculos efectuados hasta aquí serían correctos si nuestro medio de transporte se deslizase sobre la tierra. Lamentablemente, el medio en el que nos desplazamos en navegación es un fluido que se encuentra permanentemente en movimiento. Esto agrega nuevos problemas al cálculo de la posición estimada debido a dos factores:

• El viento actúa sobre la embarcación desplazándola lateralmente sobre el agua, causando el efecto que se conoce como “abatimiento”.

• El agua, que a su vez se encuentra en movimiento, altera la trayectoria y la velocidad de la embarcación, produciendo lo que llamamos “deriva”.

Estos dos factores hacen que muy rara vez el rumbo llevado sobre el fondo marino coincida con el de la proa del buque. El trayecto real seguido por la embarcación sobre la corteza terrestre (fondo marino) recibe el nombre de “derrota verdadera“ (Dv). Para determinar esta con certeza, deberemos entonces compensar las desviaciones que, tanto abatimiento como deriva, producen sobre el rumbo verdadero de la proa.

Continua en: El Abatimiento (Clase 36)

Darío G. Fernández
Director del ISNDF

30/05/2024 by Instituto Superior de Navegación

El reloj de Bitácora y la conservación del tiempo (Clase 34)

Viene de El Meridiano de cambio de fecha (Clase 33)

El Reloj de Bitácora

Muchos y muy variados fueron los intentos de construir un reloj preciso y que funcionara correctamente en el mar. A partir de los comienzos del siglo XVIII se inicia carga con un premio para aquel que pueda “hallar el medio más perfecto de conservar en la mar la igualdad de movimiento de un péndulo”, algo realmente muy complejo. Posteriormente, y gracias a la invención de John Harrison, aparecieron los primeros relojes con resorte en espiral, efectuándose las primeras pruebas con cierto éxito en un viaje de Portsmouth a Lisboa en 1736. A partir de allí, el cronómetro marino fue perfeccionado indefinidamente hasta los modernos y muy precisos relojes digitales que todos conocemos.

Nadie dudaría hoy de la confiabilidad de un buen cronómetro, pero en aquel entonces, el reloj mecánico estaba visto como un objeto poco confiable y sujeto a muchas perturbaciones.

Es bien cierto que, en la era de la navegación satelital, a pocos preocupa el no contar con un cronómetro preciso, pero es de suma importancia llevar a bordo un reloj que permita efectuar los cálculos náuticos. En la actualidad cualquier reloj moderno cuenta con la suficiente precisión como para cumplir con ese cometido. Lo ideal es utilizar un solo reloj a fin de que el horario utilizado, tanto sea para llevar la estima en la navegación, como para los cálculos astronómicos, sea siempre el mismo. En recomendable a tal efecto el llevar un reloj a bordo, en lo posible instalado en la mesa de navegación, que se utilice exclusivamente para obtener la Hora de Bitácora. Dicho reloj se llamará precisamente “Reloj de Bitácora”

La Conservación del Tiempo

Como hemos visto hasta aquí, la medición del tiempo en nuestra vida cotidiana está estrechamente ligada a los eventos astronómicos. Desde la invención del primer cronómetro se han desarrollado relojes cada vez más precisos a los efectos de poder contabilizar mundialmente el pasaje del tiempo. En el año 1949 se logra poner en marcha el primer reloj atómico que se conoce, cuyo principio de funcionamiento se basa en utilizar como contador la frecuencia de resonancia de una molécula de amoníaco, en lugar de los antiguos péndulos o resortes usados hasta entonces.

En la actualidad, los patrones de frecuencia atómicos más regulares se basan en las propiedades físicas que tienen las fuentes de emisión que poseen las moléculas de cesio. El primer reloj atómico de cesio fue construido en el Laboratorio Nacional de Física de Inglaterra en el año 1955.

Ya en el año 1967 los relojes atómicos de cesio eran lo suficientemente confiables como para que la Oficina Internacional de Pesas y Medidas los adoptara como patrón base para la definición de la unidad de tiempo a nivel internacional.

Este patrón estableció que la duración de un segundo se corresponde con 9.192.631.770 períodos de la radiación emitida en la transición entre dos niveles del estado fundamental del átomo de cesio 133. Esto hacía de los relojes de cesio los más precisos y estables que se conocían hasta el momento, admitiendo un error máximo de un segundo en 30.000 años. En la actualidad, los modernos relojes atómicos cuentan con una precisión diez veces superior, pudiendo sufrir defasajes de apenas un segundo cada 300.000 años. A partir del descubrimiento del reloj atómico se ha logrado independizar a la medición del tiempo de los fenómenos astronómicos, creando un nuevo concepto: el tiempo atómico.

El Tiempo Universal Coordinado

El Tiempo Universal Coordinado, normalmente conocido como UTC, es el sucesor del Tiempo Universal (UT), también llamado hora de Greenwich (GMT). La idea de su creación fue la de independizar el concepto de hora universal de la de una zona determinada (Greenwich), así como también la de basar su medición en parámetros atómicos en lugar de astronómicos. La hora UTC surge de comparar las diferencias horarias entre varios relojes atómicos que se encuentran funcionando en diferentes ciudades del planeta, de ahí su denominación de “coordinado”.

El seguimiento de su funcionamiento está a cargo de la Oficina Internacional de Pesos y Medidas (Bureau International des Poids et Mesures), entidad coordinadora de la metrología internacional, y se encuentra ubicada en la ciudad de París. Esta entidad se ocupa de la construcción de patrones, entre otras cosas para el kilogramo y el metro, asegurando la uniformidad internacional de las mediciones.

El tiempo universal coordinado es el que se utiliza actualmente para determinar los horarios en todo el planeta, así como también para unificar todo tipo de efemérides a nivel mundial, como por ejemplo los eventos astronómicos publicados anualmente en el Almanaque Náutico y Aeronáutico.

Continua en: Estima Directa y Estima Inversa (Clase 35)

Darío G. Fernández
Director del ISNDF

Cálculo de la Loxodromia (Clase 39)

Conceptos de Ortodromia y Loxodromia (Clase 38)

El Abatimiento (Clase 36)

Estima Directa y Estima Inversa (Clase 35)

El reloj de Bitácora y la conservación del tiempo (Clase 34)

TELÉFONO:

Cel. (011) 15 5644-2888

Sede Costanera Norte

CONTACTO