Tablas de Estima: El problema directo (Clase 40)

Viene de Cálculo de la Loxodromia (Clase 39)

Las tablas de estima son sencillamente un conjunto de tablas que traen resueltas las fórmulas para el cálculo de la derrota loxodrómica, vistas anteriormente:

Dj = D x cos R A = D x sen R tg R = A / Dj

Dichas tablas contienen todos los valores ya calculados tanto de “apartamiento” (A) como de “diferencia de latitud” (Dj) para todos los rumbos posibles tabulados de grado en grado (0o a 360o), y para distancias de 1 a 300 millas náuticas. Cada página contiene los resultados para ocho valores de “Rumbo” diferentes, cuatro en el encabezado y otros cuatro al pie. En la columna de la izquierda de cada una de las tablas aparecen tabulados los valores de distancia de milla en milla.

Las tablas de estima han caído en desuso por varias razones. La fundamental de todas ellas es que hace ya muchos años han dejado de editarse y, para obtenerlas, es preciso conseguir copias de alguien que posea algún ejemplar. Por otra parte, a partir de la invención de las calculadoras electrónicas, el método resulta un tanto más engorroso que aplicar las fórmulas matemáticas. Además, si la navegación que se pretende encarar supera las 300 millas náuticas, el cálculo completo debería hacerse por parciales. Aun así, para navegaciones cortas y en las que no se pretende excesiva precisión, resultan un método sumamente rápido y práctico. Trataremos en estas páginas de explicar su utilización, y que el lector decida qué hacer.

El Problema Directo

Como sabemos, para la resolución del problema directo contamos con los datos del punto de partida (j1 y w1), el rumbo y la distancia recorrida, y se pretende determinar las coordenadas del punto de llegada. Para ello, se busca la página que contenga el rumbo al que se navega, entre los ocho rumbos que contiene cada página. Hecho esto se ingresa, o bien por la parte superior o bien por la parte inferior con el rumbo, y por la columna de la izquierda con la distancia, debiendo extraerse los valores de Dj de la columna “N.S.” (Norte-Sur), y de apartamiento de la columna “E.W.” (Este-Oeste), tal como se aprecia en la figura No 95.

Para convertir “apartamiento” en Dw puede utilizarse una segunda tabla, llamada “Tabla 1a”, que trae precalculada la fórmula Dw = A / cos jm para todos los valores posibles de latitud media (jm) y para valores de apartamiento de 1 a 100 millas. A dicha tabla se ingresa por la parte superior con el valor de la latitud media del lugar, y por la columna de la izquierda con el apartamiento, dando como resultado el valor de Dw (fig. 96).

En la mayoría de los casos, la “Tabla 1a” no se encuentra publicada, ya que la conversión de apartamiento a Dw puede hacerse utilizando directamente las tablas de estima, aunque su uso plantea alguna complejidad adicional.

Para obtener el valor de Dw a partir del apartamiento se debe ingresar a dicha tabla con el valor de la latitud media como si fuese el rumbo, y con el apartamiento en la columna Norte-Sur (N.S.). El valor de Dw resultante se extrae de la columna de “Distancia” (Fig. 97).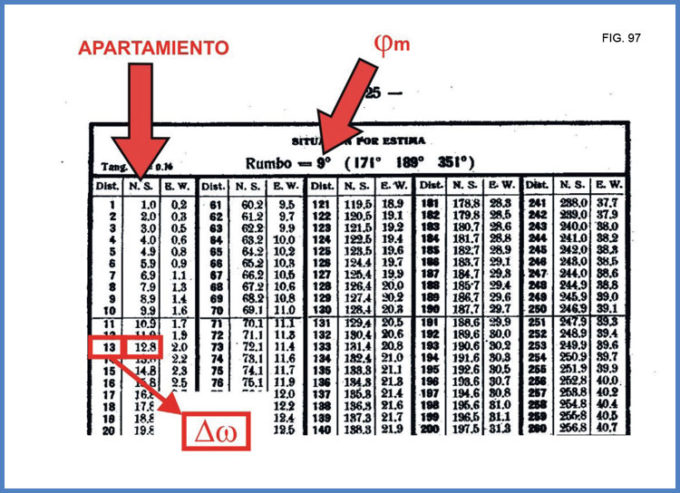 

Tal como se vio, el problema directo no presenta demasiados inconvenientes y su resolución es sumamente sencilla. El procedimiento completo sería:

• Se parte de un punto de salida con coordenadas conocidas (j1, w1).

• Se determina la distancia recorrida durante un determinado período de tiempo y el rumbo verdadero al que se navegó.

• Con los datos del rumbo y la distancia se ingresa a la tabla con el valor del rumbo en el encabezado, y el de la distancia en la columna correspondiente. Se obtienen de este modo los datos de Dj en la columna “N.S.” y de apartamiento en la columna “E.W.” (Importante: si se ingresa con el Rumbo por la parte inferior, las columnas “N.S.” y “E.W “se encuentran invertidas)

• Con el valor del apartamiento obtenido y la latitud media de la zona se ingresa a la tabla 1a y se extrae el valor del Dw. Tal como mencionábamos anteriormente, esto también puede hacerse utilizando las páginas principales.

• Hecho esto, sólo resta averiguar las nuevas coordenadas de llegada (j2 y w2) sumándole o restándole, según sea el caso, los valores de Dj y Dw obtenidos anteriormente, a las coordenadas de salida (j1, w1).

Como dijimos previamente, la fórmula Dw = A / cos jm no es del todo exacta

cuando las diferencias en latitud son importantes, debido al hecho de utilizar la latitud media como dato. Esta imprecisión se hace despreciable cuando las diferencias en latitud son mínimas. Si se pretende eliminar el error posible, las tablas de estima contienen una tabla pequeña en la primera página llamada “(1) CORRECCIÓN ADITIVA A LA LATITUD MEDIA jm PARA HACER EXACTA LA FÓRMULA A = Dw x cos jm” (Fig.98). A la misma debe ingresarse con la latitud media por la columna de la izquierda y con la diferencia de latitud por la parte superior. De la intersección entre ambas se obtiene un valor que deberá sumarse al Dw obtenido de la tabla anterior. En realidad, a los efectos prácticos, la utilización de esta tabla carece de sentido.

Para explicar la resolución del problema directo de un modo más comprensible procederemos a resolver el ejercicio de estima directa desarrollado en las páginas anteriores:

Habiendo zarpado desde j1= 32o 44,6’ S y w1= 32o 17,6’ E, y luego de haber recorrido una distancia de 282 millas náuticas a rumbo verdadero 68o. ¿Cuáles serán las coordenadas del punto de llegada?

En primer lugar, buscamos en las tablas la página que contenga los valores para el valor del rumbo 68o. Una vez allí procederemos del siguiente modo (Fig. 99):

• Se ingresa por la parte inferior con el valor del rumbo (68o).

• Se busca entre las columnas “Distancia” el valor que nos interesa. En este caso 282 millas. Debe tenerse en cuenta que, como mencionáramos anteriormente, las columnas “N.S.” y “E.W.” se encuentran invertidas respecto de los valores de rumbo de la parte superior de la tabla.

• Se extraen de la fila correspondiente los valores “N.S.” (105,6’) y “E.W.” (261,5’).

• Como ya vimos, el valor “N.S.” equivale a la diferencia de latitud (Dj), que en este caso es de 105,6’, lo que es igual a 1o 45,6’.

• El resultado obtenido de “E.W.” equivale al apartamiento. Al igual que la resolución por medio de los cálculos matemáticos, debe ahora convertirse el apartamiento en diferencia de longitud (Dw). Para ello utilizaremos la “Tabla 1a” (Fig. 100).

• Ingresamos a la tabla 1a por la columna correspondiente a la latitud media (recuerde el lector que en el ejercicio anterior habíamos adoptado una latitud media de 33o) y por la fila de la izquierda o derecha con el valor del apartamiento.

• El problema que surge aquí es que el valor máximo de apartamiento que contiene la tabla es de 100’, razón por la cual para ingresar con el valor del apartamiento obtenido (261,5’) debemos descomponerlo de la siguiente manera: 100’ + 100’ + 61’ (redondeamos 61,5’ a 61’ ya que la tabla no posee fracciones de minuto).

Para 100’ de apartamiento se obtiene una diferencia de longitud de 119,2’; mientras que para 61’ de apartamiento, la diferencia de longitud obtenida será de 78,7’. Por lo tanto Dw = 119,2’ + 119,2’ + 72,7’ = 317,1’, o sea 5o 11,1’.

Los valores obtenidos por medio de las tablas son:

Dj = 1o 45,6’ Dw = 5o 11,1

Con las fórmulas matemáticas:

Dj = 1o 45,6’ Dw = 5o 11,7’

Puede comprobarse que los resultados resultan casi idénticos a los obtenidos por el cálculo matemático. Las pequeñas diferencias se deben al hecho de redondear algunos valores a fin de usar las tablas. Para concluir el ejercicio, sólo resta sumar o restar los valores de Dj y de Dw a las latitudes de salida y de llegada, cosa que no repetiremos por haberlo hecho anteriormente.

Continua en: Tablas de Estima: el problema inverso (Clase 41)

Darío G. Fernández
Director del ISNDF

Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!