Viene de La Deriva (Clase 37)

Uno de los temas abordados con menor profundidad, tanto por las escuelas de navegación como por los textos náuticos, es el de la navegación ortodrómica. Esto se debe, probablemente, a que la mayoría de los navegantes deportivos que cruzan el océano suelen hacerlo a vela, decidiendo su travesía en función de los vientos y las corrientes más favorables. En tales casos, el hecho de recorrer una derrota más extensa probablemente no sea de vital importancia. Esto cambia de forma radical cuando se emprenden travesías prolongadas en embarcaciones a motor, donde la dirección de los vientos pierde relevancia en comparación con el ahorro de combustible. Y es ahí donde el concepto de navegar por el círculo máximo se torna de suma importancia, debido a las enormes distancias que pueden acortarse llevando el barco por la ruta correcta.

Ortodromia y Loxodromia

Sabemos que la distancia más corta entre dos puntos que se hallan ubicados sobre una superficie plana es la recta que une ambos puntos. Sobre la superficie terrestre, que es en realidad una esfera, esto podría considerarse válido solo para distancias relativamente cortas. Si, en cambio, se deben unir dos puntos que se encuentran ubicados sobre una esfera y que mantienen una separación importante entre sí, la distancia más corta entre ambos será el arco de círculo máximo que contiene a dichos puntos.

Podríamos definir al círculo máximo como al círculo resultante de intersectar a una esfera con un plano que contenga al centro de la misma. Hablando particularmente de la esfera terrestre, son círculos máximos los meridianos y el Ecuador pero no así los paralelos. Estos últimos son círculos menores, paralelos al Ecuador, pero que no contienen al centro de dicha esfera.

En el esquema de la figura No 90 se han representado los puntos “A” y “B” sobre la superficie terrestre. Aunque a priori puede pensarse que la distancia más corta entre ambos puntos es la línea que los une recorriendo su paralelo (representada en color verde), esto es absolutamente falso. La distancia mínima entre ambos corresponde al arco (representado en color rojo) perteneciente al círculo máximo, que contiene a los puntos en cuestión y que a su vez pasa por el centro de la esfera. Esta última línea recibe el nombre de “derrota ortodrómica” o simplemente “ortodromia”, mientras que a la primera se la denomina “loxodromia”.

En realidad podemos definir a la loxodromia como aquella línea sobre la que navega un buque manteniendo su rumbo constante.

Debido a que la derrota loxodrómica corta a todos los meridianos con igual ángulo, ésta puede ser representada como una línea recta en una carta de proyección Mercator (Fig. 91). La derrota loxodrómica, aunque no es la distancia menor entre dos puntos de la esfera, es siempre preferible a la ortodrómica para distancias no demasiado extensas, debido a la sencillez del procedimiento de navegar a rumbo constante. La derrota ortodrómica, si bien representa a la distancia más corta, tiene la desventaja de que su rumbo no es regular, es decir que el ángulo con el que corta los meridianos va variando, por lo que no puede ser representada como una línea recta en una carta mercatoriana. En dichas cartas, la ortodromia queda representada por una curva con su concavidad hacia el Ecuador y su convexidad hacia los polos. La derrota ortodrómica se verá como una línea recta solo en las cartas de tipo gnomónicas ya que en éstas, y dado que el punto de vista se encuentra en el centro de la esfera, todos los círculos máximos también son rectas. En las cartas con proyección gnomónica, las loxodromias se verán como curvas con su concavidad hacia los polos debido a que siguen la curvatura de los paralelos.

En la figura No 92 puede verse claramente cómo en una ortodromia el rumbo va variando (en este caso aumentando) a medida que atraviesa los diferentes meridianos (R5 > R4 … > R1), mientras que en la loxodromia se mantiene el rumbo constante (R1 = R2 = … = R5). En este último caso puede comprobarse que navegando a rumbo permanente sobre la esfera terrestre, la derrota resultante sería la de una curva que se aproxima cada vez más a alguno de los polos, conformando un recorrido espiralado.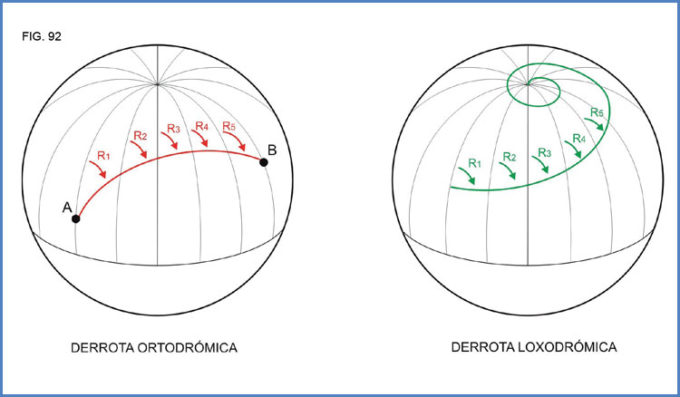

Cuando se navega con cartas con proyección Mercator de zonas reducidas está claro entonces que la manera conveniente de navegar será por la Loxodromia; pero en el caso de navegaciones más extensas será conveniente definir cuál será la derrota más apropiada a seguir. Para ello será necesario hacer un análisis acerca de si la distancia a recorrer sobre la ortodromia es suficientemente menor que sobre la loxodromia, como para justificar así la utilización de la primera. En tal caso, el método a seguir será el de calcular ambas distancias, tanto la loxodrómica como la ortodrómica, y efectuar luego la comparación entre ambas. A continuación, desarrollare-mos en profundidad ambos métodos.

Continua en: Cálculo de la Loxodromia (Clase 39)

Darío G. Fernández
Director del ISNDF

Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!