Cuando comienza en Europa el período de las grandes navegaciones oceánicas, y gracias al descubrimiento del Nuevo Mundo, se vuelve imprescindible el perfeccionar los métodos conocidos hasta entonces para determinar la situación de los barcos en el mar. La obtención de la latitud geográfica no presentaba por entonces mayores problemas y la mayoría de los navegantes contaba ya con varios métodos para establecerla con bastante precisión. No ocurría lo mismo con la longitud, y su determinación precisa se volvió una obsesión tanto para navegantes como para cosmógrafos, astrónomos e incluso para algunos reyes que veían peligrar las riquezas obtenidas en sus nuevos dominios.
Los primeros intentos
Según parece, el primero que ideó un sistema de coordenadas más o menos parecido al que hoy conocemos fue Hiparco, proyectando en la esfera terrestre las coordenadas utilizadas en la esfera celeste. Habría sido él mismo quien intentó un método para la determinación de la longitud empleando los eclipses de Luna, aunque nada concreto aparece hasta principios del siglo XVII.
Se sabe con certeza que uno de los primeros en intentar resolver el problema fue el célebre Galileo, quien propuso al Rey de España un método bastante curioso. El mismo se basaba en su reciente descubrimiento de los satélites de Júpiter, e intentaba establecer la longitud geográfica por medio de la observación de los eclipses y ocultaciones a que se veían sometidos los satélites jovianos. El problema que enfrentaba no era poca cosa: el instrumento necesario para visualizar las lunas de Júpiter precisaba de un aumento importante y, por otra parte, debía contar con un enorme campo visual para contrarrestar los movimientos de los barcos en el mar. Aun así, se hacía sumamente difícil la observación. El propio Galileo ideó un artefacto especial, al que le siguieron varios más. Entre otros, un tal Bouguer, construyó a tal efecto un anteojo de tres metros de longitud pero sin resultados satisfactorios.
Algunos otros intentaron por otro camino. En 1567, Jacobo Besson invento lo que llamó “el asiento del observador”, que no era otra cosa que una tabla colgante que minimizaba las sacudidas en el mar. A éste lo siguieron muchos otros inventores, ideando un sinnúmero de estrambóticos mecanismos que combinaban todo tipo de anteojos con sillas de tipo cardánica.
Por entonces, algunos cosmógrafos propusieron otros métodos basados en los eclipses solares, e incluso se pensó en los lunares, aunque todos ellos nunca llegaron a ser una realidad en la resolución del problema. El inconveniente no sólo residía en la dificultad de la observación, sino también en que los eclipses, tanto sea lunares como solares o jovianos, son poco frecuentes con relación a lo que el navegante necesita.
Aun así, muchos continuaron insistiendo en el método de Galileo hasta bien entrado el siglo XIX.
El método del almirante

Quien creyó haber descubierto por fin el método para la determinación de la longitud, o como la llamaban en la España de la época: altura del este – oeste, fue el mismísimo Cristóbal Colón. Fue durante su primer viaje en que comenzó a notar que la declinación magnética variaba a medida que avanzaba hacia el poniente, a la vez que pasaba del Este al Oeste a la altura del meridiano de los 3º W.
La noche del 13 de septiembre de 1492 anotó en su diario de bitácora: “Aquel día con su noche, yendo a su vía, que era el Oeste, anduvieron 33 leguas, y contaba 3 o 4 menos. Las corrientes le eran contrarias. En este día, al comienzo de la noche, las agujas nordesteaban, y a la mañana noroesteaban algún tanto”. Esta claro que percibió la variación de la declinación utilizando la estrella polar.
Don Cristóbal comenzó entonces a efectuar minuciosas anotaciones acerca de la declinación magnética de las zonas por las que navegaba, convencido de que, determinando su variación, podía establecer la longitud en la que se encontraba. De poco le valió su trabajo en ese sentido ya que, como sabemos, la declinación no varía de manera lineal sobre la esfera terrestre así como tampoco es constante a través del tiempo. De más está decir que su método fracasó rotundamente aunque, sin proponérselo, bosquejó los primeros mapas con líneas “isógonas” (líneas que unen puntos de igual declinación magnética) que se conocen. Algo que más tarde sería de suma utilidad.
Algún tiempo después aparecieron muchos otros proyectos similares al de Colón, e incluso hubo alguno que intentó utilizar la “inclinación” de la aguja en lugar de la “declinación”, pero todos ellos resultaron inútiles a los fines que se pretendía.
Un curioso concurso
El enorme desarrollo naval aparecido en Europa después de la conquista, hacía del problema de la longitud una cuestión de estado. Nada era más importante por entonces, a punto tal que algunos soberanos comenzaron a ofrecer suculentos premios a aquellos que pudiesen proveer a su majestad de un método eficiente para determinar la longitud. El primero en intentar este camino fue Felipe III, un siglo antes que sus predecesores, ofreciendo la suma de 6000 ducados de renta permanente más algunos adicionales a aquel que descubriese un método eficaz.
Lamentablemente no era el momento científico más propicio y la iniciativa no tuvo buenos resultados, pero fue tal la popularidad que tomó el concurso que aparecieron miles de aspirantes de toda Europa con métodos de los más disparatados. De entre todos ellos, pocos tenían real sustento científico como el aportado por Galileo Galilei, a quien ya mencionamos. Otros países sucedieron en la iniciativa a Felipe III casi un siglo después, entre ellos Francia, Inglaterra y Holanda. El más importante de todos fue el que estableció el Parlamento inglés en 1714, al que se conoció como “Premio de la Reina Ana”.
Lo curioso de este concurso residía en el reparto de los premios, que quedaban establecidos de la siguiente manera: 20.000 libras esterlinas al método que permitiera determinar la longitud en el mar con un error de medio grado, 15.000 si el error rondaba los dos tercios de grado, y sólo 10.000 si la imprecisión superaba el grado.
Según parece, fueron tantas y tan insólitas la mayoría de las propuestas recibidas, que fue necesaria la publicación de una explicación completa de lo que se entendía por longitud, ya que en muchos casos los disparates pergeñados por algunos ni siquiera tenían que ver con la posición en el mar.
De entre todos los sistemas presentados a su majestad, apareció uno que se utilizó con éxito hasta hace no mucho tiempo: el método de las distancias lunares.
Las distancias lunares
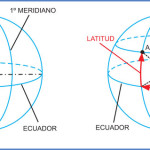
No es objeto de esta nota explicar un método tan complejo, pero vamos a intentar que se comprenda al menos la idea principal. Como sabemos, la tierra da una vuelta completa (360º) cada 24 horas. Un cálculo simple nos permite establecer que el Sol recorre 15º de longitud en una hora. Digamos además que el Sol debería pasar tanto por el primer meridiano como por el de cualquier observador aproximadamente a las 12:00 hs. hora civil.

Pues bien, determinando el momento en que el Sol atraviesa el meridiano del observador y conociendo la hora del primer meridiano en ese mismo momento, se puede establecer por diferencia horaria, el tiempo que el Sol tardó en llegar desde el meridiano de origen hasta la supuesta posición. Hecho esto, es fácil conocer la longitud aplicando una sencilla regla de tres. Por ejemplo, si el Sol tardó en recorrer desde el primer meridiano hasta nuestra posición 2 hs. 20 min., podemos decir que:
Si en 60 min. (1 hora) ______________ 15º
en 140 min. (2 h. 20 m.) _____________ 140 x 15 / 60 = 35º
Conclusión: si el Sol se encuentra ahora en el meridiano del observador y son las 14:20 hs. en el primer meridiano, éste habrá tardado 2 hs. 20 min. en desplazarse desde éste hasta la nueva posición. Por lo tanto habrá recorrido 35º, siendo éste el valor de la longitud del observador. El sistema aparenta ser sumamente sencillo, y de hecho lo es, salvo por la imposibilidad de determinar la hora del meridiano de 0º, y esto se debe a una razón muy simple: aún no se había inventado el cronómetro.
Pues bien, el método de las distancias lunares sirve concretamente para determinar esto último (la hora del primer meridiano), utilizando para ello la posición de la Luna y de un astro cualquiera. Se llama “distancia lunar” al ángulo formado entre la visual desde un punto cualquiera de la Tierra, a los centros de la Luna y al astro en cuestión. Obteniendo dicho ángulo por medio de un instrumento óptico y recurriendo a las efemérides anuales se podía, luego de varias correcciones, determinar la hora de Greenwich en ese instante.
Este método ya había sido propuesto por Nüremberg en el año 1514, aunque el que vio la luz fue el aportado por Morín en 1634. El problema de la precisión del método ya no residía en la observación sino en la confección de tablas que contengan las efemérides de la Luna. Esto preocupó y mantuvo ocupados a todos los genios de la época, a punto tal que en la construcción de almanaques náuticos precisos intervino el mismísimo Isaac Newton. Toda la ciencia náutica se encontraba abocada a una sola tarea: la construcción de una tabla de la Luna. Dálembert, Clairaut, Euler, Halley y el propio Newton aportaron lo necesario y fueron cientos las tablas que comenzaron a publicarse entre los distintos países.
El misterio de la longitud comenzaba a develarse.
Los nuevos relojes
El método de las distancias lunares para determinar la hora del primer meridiano tuvo su apogeo en los comienzos del siglo XIX, cayendo lentamente en desuso por varias razones. Una de ellas era que los cálculos de paralaje, refracción y semidiámetro, convertían al método en algo sumamente complejo para los nuevos navegantes. Por otra parte, la invención de los relojes mecánicos hacía inútil al sistema. Para obtener la hora del primer meridiano sólo era necesario contar con uno de estos modernos artefactos, ajustarlo a la hora del meridiano de referencia y mantenerlo funcionando a bordo. Curiosamente, el método se continuó utilizando en algunos países hasta casi finales del siglo XIX. Incluso en nuestro país, dicho sistema aparece explicado en los libros de la Escuela Naval Militar editados en el año 1909.
Una interesante curiosidad reside en que el descubrimiento del método de las distancias lunares ocurre casi al mismo tiempo que se desarrollan las primeras teorías sobre relojes mecánicos. De hecho, en una junta celebrada en Badajoz en 1524, Fernando Colón (hijo de Cristóbal) propuso el método de los relojes para determinar la longitud, expresando lo siguiente: “La otra forma sería crear un instrumento fluente, el cual, en el más largo y determinado espacio de tiempo que se pudiera, acabase de correr asignando en él sus puntos divisos por sus horas y cuartas y fracciones (habla concretamente de inventar un reloj), y con el instrumento comenzar a caminar desde el lugar donde comienza la partición al punto de mediodía (hora del primer meridiano), y cuando caminase más al Oriente por cada quincena parte hora que el mediodía viniese al caminante antes de haber recorrido 24 horas, diremos que había caminado un grado hacia el Oriente o por el contrario hacia el Occidente”.
Gemma Fissio, célebre cosmógrafo y matemático de la época, lo explica de un modo mucho más simple: “Antes de poneros en camino, poned vuestro reloj a la hora del lugar que vais a dejar; cuidad de que la máquina no se pare durante el trayecto; cuando tengáis corridas veinte leguas, por ejemplo, hallad la hora del lugar con el astrolabio, esperando para ello que la sombra caiga justamente sobre la línea horaria; comparad esta hora con la de vuestro reloj y tendréis la diferencia en longitud”. Más claro, imposible.
Muchos y muy variados fueron los intentos de construir un reloj preciso y que funcionara correctamente en el mar. A partir de los comienzos del siglo XVIII se inicia una verdadera carrera en la construcción y perfeccionamiento del cronómetro marino. Al comienzo sólo fueron fracasos ya que se intentaba fabricar un reloj marino utilizando para ello el péndulo como sistema. En 1720 la Academia de París vuelve a la carga con un premio para aquél que pueda “hallar el medio más perfecto de conservar en la mar la igualdad de movimiento de un péndulo”, algo realmente muy complejo.
Posteriormente aparecieron los primeros relojes con resorte en espiral, efectuándose las primeras pruebas con cierto éxito en un viaje de Portsmouth a Lisboa en 1736. A partir de allí, el cronómetro marino fue perfeccionado indefinidamente hasta los modernos y muy precisos relojes digitales que todos conocemos.

Nadie dudaría hoy de la confiabilidad de un buen cronómetro, pero en aquel entonces, el reloj mecánico estaba visto como un objeto poco confiable y sujeto a muchas perturbaciones. Esa fue tal vez la razón por la cual, el método de las distancias lunares, continuó vigente tantos años después de inventado el cronómetro. El ocaso definitivo de las distancias lunares se produce cuando, en 1837 y casi por casualidad, el Capitán Thomas Hubbard Sumner realizó el descubrimiento de las rectas de altura, pero esa ya es historia para el próximo artículo.
Es bien cierto que, en la era de la navegación satelital, a pocos preocupa el no contar con un cronómetro preciso además de un buen sextante. Es posible, pero coincidirá conmigo el lector en que aquel que pueda disponer de más de un método de posicionamiento, navegará mucho más tranquilo. En tal sentido les dejo una frase que encontré y que me resultó muy interesante: “Por más útiles que sean actualmente estas máquinas y por más que se perfeccionen en lo sucesivo, es evidente que siempre quedarán sujetas al efecto de los accidentes extraños, y que los buenos principios de la construcción, nunca las liberarán de ciertas irregularidades en su movimiento. El cúmulo de estas irregularidades, con el tiempo, puede producir errores considerables; así, el uso de estos artefactos exige mucha prudencia, y nunca deberá considerarse ni emplearse como método único”.
¿Creyó que hablaba del GPS? Se equivoca. Este texto pertenece al “Tratado de Navegación”, publicado en 1787 por el Capitán Mendoza, y hacía alusión a los cronómetros marinos. Una interesante analogía con nuestros modernos navegadores satelitales. Pura coincidencia.
Darío G. Fernández
Director del ISNDF
 Curso de Timonel: Coordenadas Geográficas (Clase 41)
Curso de Timonel: Coordenadas Geográficas (Clase 41) Latitud y longitud (clase 4)
Latitud y longitud (clase 4)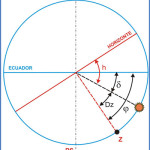 La longitud en el mar (parte 2)
La longitud en el mar (parte 2) Las distintas proyecciones cartográficas III
Las distintas proyecciones cartográficas III Las distintas proyecciones cartográficas II
Las distintas proyecciones cartográficas II