Viene de: Curso de Timonel: Sudestada, Pampero y Nortazo (clase 40).
A pesar de lo que muchos creen, la tierra no es una esfera perfecta sino que su forma es un “geoide” (esfera achatada en los polos). La misma gira en sentido “directo” (sentido horario vista desde el Polo Sur) alrededor de un eje que atraviesa los polos. Los hombres, deseosos de situarse en la esfera terrestre de manera eficaz, diseñaron un método basado en el trazado de líneas verticales y horizontales que conforman sobre la superficie de la esfera terrestre una especie de reticulado, útil para posicionarse en cualquier punto del planeta. A este sistema de líneas verticales y horizontales se lo conoce con el nombre de “coordenadas geográficas”.
Coordenadas geográficas
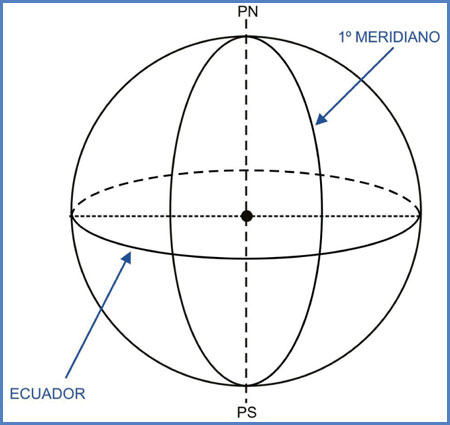
Si cortamos a la esfera terrestre con un plano “perpendicular” al eje de la misma, donde su intersección genere un círculo máximo habremos definido el “Ecuador terrestre”. Los paralelos (líneas paralelas al Ecuador), estarán conformados por otros planos que en su intersección con el contorno terrestre generan círculos menores. A su vez, si cortamos a la esfera terrestre en sentido vertical con infinitos planos que “contengan” a su eje, obtendremos círculos máximos llamados meridianos. Estos, a diferencia de los paralelos, convergerán en dos puntos llamados Polo Norte y Polo Sur.
Se adoptó por convención como 1º meridiano al que pasa por la localidad inglesa de Greenwich, a partir del cual se puede ubicar un punto en la esfera midiendo el ángulo central que se forma desde este último hasta el punto en cuestión, que será de 0º hasta 180º, ya sea en sentido Este u Oeste. A esta coordenada se la conoce como Longitud. A su vez, a partir del Ecuador puede situarse una posición determinada midiendo el ángulo central que se forma respecto de este y hacia los polos, y será de 0º a 90º ya sea en sentido Norte o Sur. Esta será entonces la coordenada Latitud. Quedará así perfectamente definida la posición del punto “A” en la figura, por las coordenadas latitud y longitud, que serán en definitiva los ángulos centrales medidos desde el Ecuador y desde el meridiano de Greenwich, respectivamente.

La tierra queda entonces dividida en dos mitades en sentido Norte-Sur a partir de la línea del Ecuador. La semiesfera comprendida entre el Ecuador y el Polo Norte recibirá el nombre de hemisferio Norte, mientras que la otra recibirá el nombre de hemisferio Sur. En el sentido Este-Oeste, los hemisferios resultantes de la división formada respecto del 1º meridiano se llamarán hemisferio occidental y hemisferio oriental, respectivamente.
Continua en: Curso de Timonel: Cartas Náuticas (clase 42).
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de timonel completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!