Viene de: La latitud y la Estrella Polar (parte 2).
La altura meridiana de cualquier cuerpo celeste es la máxima altura que dicho cuerpo puede alcanzar por sobre el horizonte y se produce precisamente en el instante en que atraviesa el meridiano del observador. Todos sabemos que el Sol asoma por el Este y va ganando altura hasta que alcanza su máximo, en horas cercanas al mediodía, momento a partir del cual su altura comienza a decrecer hasta el ocaso. Pues bien, al momento de su máxima altura, también llamado “culminación”, el Sol se encuentra exactamente en la línea Norte-Sur del navegante, es decir, en su meridiano. Esta particularidad hace que sea muy sencillo calcular el valor de la latitud, simplemente obteniendo la altura máxima del astro durante su culminación, de manera independiente de la hora en que ésta se produzca.
En el esquema se ha graficado a un observador y a un astro durante su culminación, ambos en el hemisferio Norte, en el que pueden apreciarse los siguientes elementos:
- Horizonte. Como puede comprobarse, éste es un plano que se encuentra a 90º de la vertical del observador, tal como ocurre en la realidad.
- La altura del astro (h). Esta es en definitiva la altura que el navegante puede medir con su sextante y no es otra cosa que el ángulo que verá el navegante entre el astro y el horizonte.
- La declinación del astro (δ). Para aquellos que no están demasiado familiarizados con la astronavegación, la declinación de un astro es el equivalente a la latitud, pero en la esfera celeste. Puede comprobarse en el esquema que la declinación es el arco de meridiano comprendido entre el Ecuador y el astro.
- La latitud del observador (ϕ). Es lo que se desea averiguar.
- La distancia zenital (Dz). Para explicarlo de un modo sencillo, podríamos decir que es la distancia angular que existe entre el zenit del observador y el astro en cuestión. Como puede comprobarse, entre el zenit del observador y el horizonte hay 90º, por lo tanto la distancia zenital y la altura son ángulos complementarios (Dz + h = 90º). Debido a la dificultad de medir la distancia zenital de manera directa, ya que se hace imposible identificar al zenit en el cielo, para obtener su valor se procede midiendo su altura por sobre el horizonte y se resta el valor obtenido a 90º (Dz = 90º – h).
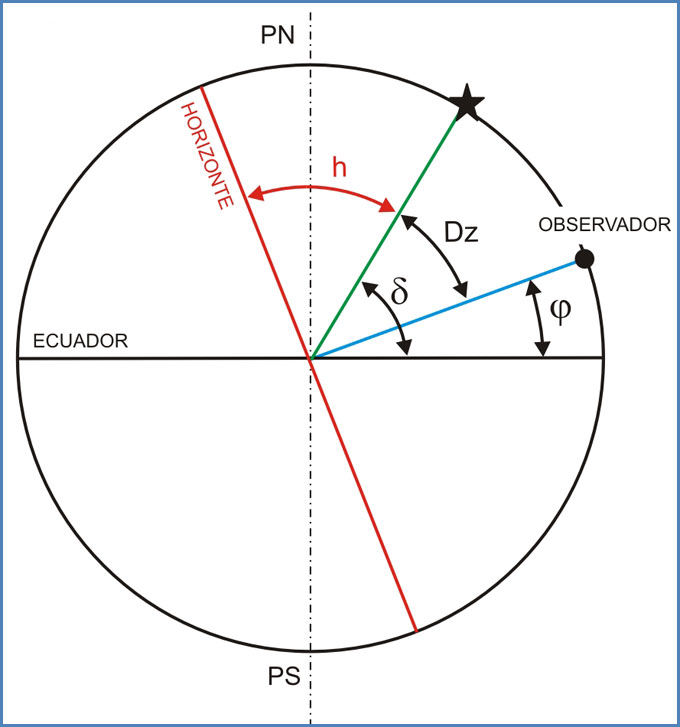
Del gráfico se desprende claramente que el valor de la latitud del observador, en este caso en particular resulta de restar, en valor absoluto (sin el signo), la declinación (δ) del astro para ese instante, y la distancia zenital (Dz) al mismo.
ϕ = δ – Dz
Dependiendo de las posiciones relativas que tenga tanto el observador como el astro, la fórmula variará, pero en todos los casos la latitud resulta de sumar o restar la declinación del astro y la distancia zenital.
El cálculo de la latitud utilizando la altura meridiana del Sol era, junto con la altura de la estrella polar, la única herramienta más o menos precisa de que disponía el navegante por aquellos tiempos. De hecho, la obtención de la latitud era de vital importancia ya que se hacía imprescindible para obtener la longitud. El método más frecuentemente utilizado, ya en la era del cronómetro, para obtener la longitud era el método conocido como el de las “alturas cronometradas”, antes mencionado. El mismo consistía en obtener la altura del Sol en un momento en el que este se encontrara muy próximo al Este o al Oeste (azimut 90º ó 270º) y se tomaba nota de la hora de la observación. Hecho esto, el navegante calculaba su nueva latitud a partir de la latitud obtenida en la meridiana, utilizando para ello los cálculos de estima habituales. A partir de este punto ya podía calcular, aplicando la trigonometría, el ángulo horario local del astro (AHL) utilizando la fórmula:
cos AHL = (sen h – sen ϕ . sen δ) / cos ϕ . cos δ
Una vez obtenido el AHL, era muy sencillo determinar la longitud (ω) teniendo como dato el AHG (longitud) del Sol:
ω = AHG +/- AHL
Este procedimiento era el más utilizado por los navegantes de la época previa al descubrimiento de la recta de altura, y fue el que utilizó el Capitán Thomas Hubbard Sumner cuando, accidentalmente, dio con la primera línea de posición astronómica. Tal era la importancia del cálculo de la latitud por altura meridiana del Sol, que existían varios métodos a partir de los cuales se podía obtener la altura meridiana, si por alguna razón (generalmente nubes) no se hubiese podido obtener la altura del Sol al momento de su culminación. Algunos de los más usuales son:
- • Latitud por altura circunmeridiana (hcm): Se define como altura circunmeridiana a la altura de un astro que se encuentra próximo a su culminación, tanto sea antes como después. El procedimiento consiste en determinar la corrección que debe aplicarse a la altura circunmeridiana obtenida, para convertirla en altura meridiana (hm).
Para obtener dicha corrección es necesario previamente calcular el tiempo que media entre la altura circunmeridiana obtenida y la hora en que debería producirse el pasaje meridiano (t). Una vez calculado dicho tiempo, la corrección surge de un sencillo cálculo matemático utilizando para ello la fórmula:
hm = hcm + a.t2
Donde:
“hm” es la altura meridiana que se desea averiguar.
“hcm” es la altura circunmeridiana obtenida un tiempo anterior o posterior a la culminación.
“a” es un coeficiente que representa la variación en altura que presentará el astro en el minuto que sigue o que precede al paso meridiano.
“t” es el tiempo transcurrido entre la hora en que se tomó la altura circunmeridiana y la hora en que se supone se produciría el pasaje meridiano.
Sin entrar en análisis demasiado complejos, queda claro que la fórmula expresa lo siguiente: conociendo lo que varía el astro en altura en el minuto próximo a la meridiana (“a”), y conociendo también el intervalo de tiempo entre dicha meridiana y el instante en que se tomó la circunmeridiana (“t”), es sencillo calcular cuál será su variación total. Por supuesto que dicha variación no es lineal sino que es exponencial y está dada por el factor a.t2.
Algunos años más tarde, dicho cálculo ya fue incluido en tablas que facilitaban enormemente el trabajo del navegante. Cabe aclarar que para que el procedimiento gozase de cierta precisión, es menester que el tiempo (t) antes mencionado no excediera ciertos límites, también estipulados en las tablas de cálculo.
- Latitud por altura extrameridiana: En el caso de que no se hubiese podido obtener una altura meridiana o una circunmeridiana dentro de los límites establecidos a tal efecto, es posible reducir a meridiana una altura tomada fuera de los límites mencionados, aplicándole a dicha altura una corrección adicional. De cualquier modo, la latitud obtenida por altura extrameridiana no ofrece garantías de precisión.
- Latitud por dos alturas circunmeridianas y el intervalo: Este procedimiento, muy poco utilizado, se basaba en obtener dos alturas circunmeridianas, una anterior y la otra posterior al pasaje meridiano, y promediar sus correcciones en función de sus respectivos tiempos.
Todos estos procedimientos complejos y poco precisos destinados a obtener la latitud, quedaron obsoletos y cayeron completamente en desuso cuando vio la luz la primera línea de posición astronómica, también llamada recta de altura. A partir de tal descubrimiento ya no era necesario calcular la latitud y la longitud de manera separada y el arte de navegar consistía en trazar rectas de altura e intersectarlas hasta lograr un FIX. A tal efecto, tanto la altura circunmeridiana como la extrameridiana resultaban mucho más útiles empleándolas en el cálculo de una recta de altura convencional que reduciéndolas a meridianas, lográndose así una mayor precisión en el resultado final.
De cualquier manera, el procedimiento para obtener la latitud por altura meridiana sigue siendo interesante por su simplicidad y rapidez de cálculo.
Darío G. Fernández
Director del ISNDF
