Viene de La navegación costera: Linea de posición – segunda parte (Clase 45)
Como ya sabemos, la visual al horizonte depende estrictamente de la altura del punto de observación. Está claro que cuanto más alto se encuentra nuestro ojo, más lejos podemos divisar. Y esto se debe a que la distancia al horizonte queda determinada por un cono, cuyo vértice es el ojo del observador y su base es una circunferencia. Dicha circunferencia queda definida donde los lados del cono (la línea de la visual) cortan tangencialmente a la corteza terrestre. De ahí que a mayor altura, mayor es la distancia al horizonte. (Fig. 119).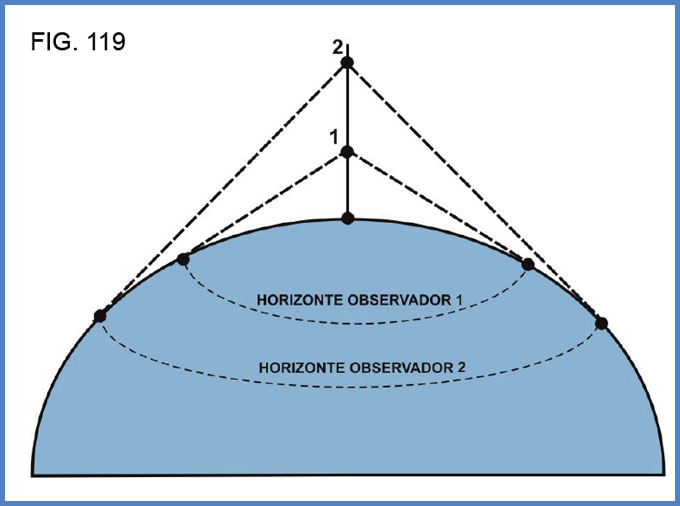
Pues bien, dado que la distancia al horizonte depende exclusivamente de la altura a la que se encuentre el observador, existe un procedimiento que permite determina dicha distancia en función de la elevación de ojo. Analicemos el esquema de la figura No 120.
O = Ojo del observador R = Radio terrestre H = Altura de ojo del observador D = Distancia visual al horizonte d = Distancia terrestre al horizonte
Aquí se ha representado a una porción de la superficie terrestre y a un observador cuyo ojo se encuentra en “O”. “H” representa la altura a la que se encuentra dicho ojo, mientras que “R” es el radio terrestre. La distancia visual al horizonte está representada por “D”, mientras que la distancia terrestre es el arco “d”.
Si bien lo que nos interesa calcular es la distancia “d” en función de la altura de ojo, la primera conclusión que surge del gráfico es que “D” y “d” pueden considerarse perfectamente idénticas en la práctica ya que, para la distancia en cuestión, la curvatura terrestre bien podría considerarse nula, y la altura de ojo es despreciable en relación a la distancia. Por esa razón, estableciendo el valor de “D” estaríamos indirectamente calculando “d”.
Como puede apreciarse, se ha formado un triángulo rectángulo cuyos lados son: El lado “R”, el lado “D” y el lado “R” + “H”. Por teorema de Pitágoras (“El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”) tenemos que:

Dado que la altura de ojo en relación al radio terrestre puede considerarse nula, el término H2 puede perfectamente eliminarse.
Entonces: 
Reemplazando el valor del radio terrestre (en metros) en la fórmula, obtendremos que la distancia al horizonte, expresada en metros, será:

Si queremos expresar el valor de la distancia en millas náuticas, entonces:
Esta sería la ecuación final de no mediar los efectos de la “refracción geodésica”. Dicho fenómeno hace que los rayos luminosos se vean desviados de su trayectoria, producto del cual el horizonte visible se extiende un tanto más allá de lo que permite la curvatura terrestre. En definitiva, el efecto que provoca es que veamos una parte del horizonte que se encuentra oculta. De ahí que al “horizonte marino” se lo conozca también con el nombre de “horizonte aparente”.
Para tener en cuenta el efecto causado por la refracción geodésica en la fórmula, se deberá incluir la expresión:
1 – 2 xg
Donde “g“ es el coeficiente de refracción media. Este valor, para condiciones atmosféricas normales, es de 0,08.
Volviendo al desarrollo anterior y agregando la corrección por refracción geodésica tendremos que:
Expresado en millas será:

Esta es la fórmula por todos conocida para establecer la distancia al horizonte visible desde una altura de ojo determinada. Supongamos como ejemplo que nos encontramos con una elevación de ojo de 7 metros. Reemplazando dicho valor en la fórmula, tendremos que:
Con el mismo propósito, existen tablas que permiten obtener de manera directa el valor de la distancia al horizonte aparente, ingresando simplemente con el valor de la altura del punto de observación (Fig. 121).
Como puede apreciarse, el resultado obtenido aplicando cualquiera de ellas es idéntico al obtenido matemáticamente. Lamentablemente, este tipo de tablas ya no se editan en nuestro país y, para obtenerlas, es preciso recurrir a fotocopias de volúmenes antiguos de la Escuela Naval Militar (al frente en la figura).
Existen países donde aún se continúan editando diversos compilados de tablas útiles para la navegación. Una opción interesante son las Norie’s Nautical Tables inglesas (al fondo en la figura).
Continua en: Distancia a un faro cuyo tope se ve en la línea del horizonte (Clase 47)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestros teléfonos 4383-3843/4395, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!