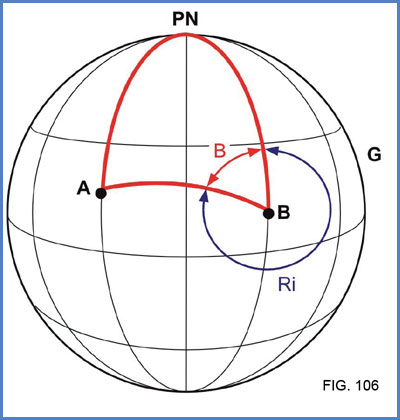
Viene de La Derrota Ortodrómica: El Triángulo Terrestre (Clase 42)
A fin de ejemplificar el cálculo retomaremos la navegación planteada anteriormente y la calcularemos navegando por el círculo máximo.
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestros teléfonos 4383-3843/4395, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!
