Viene de Tablas de Estima: El problema directo (Clase 40)
El Problema Inverso
La resolución de la estima inversa por medio de las tablas presenta alguna complejidad adicional, si bien el procedimiento acaba resultando sencillo una vez familiarizados con su utilización. Como sabemos, el problema inverso plantea el poder determinar el rumbo verdadero al que se deberá gobernar para unir dos puntos con
coordenadas conocidas, y la distancia que media entre ambos. A los efectos de mejorar la comprensión del lector resolveremos el ejercicio anterior, pero esta vez utilizando las tablas de estima:
• Determinar el rumbo verdadero que se deberá seguir y la distancia a recorrer para navegar desde el puerto de Montevideo, cuyas coordenadas aproximadas son j = 34o 54,5’ S y w = 56o 7,6’ W, hasta Ciudad del Cabo, con coordenadas j = 33o 20,3’ S y w = 18o 25,6’ E.
Dado que sabemos de antemano las coordenadas de salida (j1, w1) y de llegada (j2, w2), calcularemos los valores de Dj y de Dw al igual que lo hicimos por medio de las fórmulas matemáticas:
Dj = j1 – j2 Dj = 34o 54,5’ – 33o 20,3’ Dj = 1o 34,2’ Dw = w1 + w2 Dw = 56o 7,6’ + 18o 25,6’ Dw = 74o 33,2’
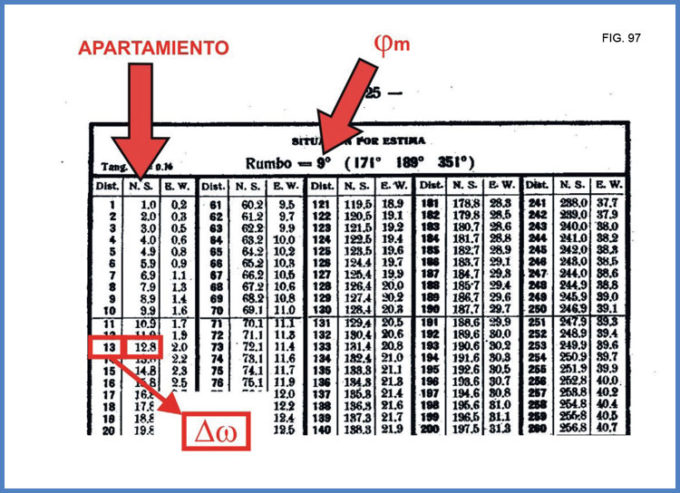
Acto seguido se debe determinar el apartamiento. Para ello debe ingresarse en la tabla 1a con la latitud media de la zona (34o) por la parte superior y descender por la columna de diferencia en latitud hasta encontrar el valor de Dw correspondiente. Una vez allí, hay que desplazarse por la fila hacia la izquierda o hacia la derecha hasta encontrar el dato del apartamiento. De no contar con dicha tabla, utilizaremos las páginas principales de la siguiente manera (Fig. 101):
• Ingresamos a la página correspondiente con el valor de la latitud media como si fuera el “Rumbo” (en nuestro caso 34o).
• Una vez hallada la página correspondiente, se ingresa con el valor de Dw, expresado en minutos (74o 33,2’ = 4.473,2’) en la columna “Distancia”, y se obtiene el apartamiento en la columna “N.S.” Aquí ya nos surge una primera complicación: en nuestro caso, el valor
de Dw supera los valores máximos tabulados, ya que el máximo que encontraremos en dicha columna será de 300 millas. Para resolver el dilema utilizaremos la décima parte de Dw, es decir 447’. Al resultado obtenido habrá que multiplicarlo luego por 10.
• Dado que aun así superamos el valor máximo, deberemos descomponer nuestro Dw (447’) en dos partes: por un lado ingresaremos con el valor 300’ y por el otro con 147’.
• Los datos extraídos en la columna “N.S.” simplemente se suman y se multiplican por diez (no olvidar que se ingresó a la tabla con la décima parte de Dw)
A = (121,9’ + 248,7’) x 10
A = 3.706 Mn.
Repetimos nuevamente que es sumamente importante prestar atención a los encabezados de las columnas, ya que cuando se ingresa, como en este caso, tanto con la latitud media como con el rumbo por la parte superior, deben tenerse en cuenta los encabezados de las columnas de arriba; mientras que si se ingresa con los rumbos o latitudes medias que aparecen al pie de la tabla, los encabezados de cada columna deben leerse de la parte inferior. Pues bien, lo que sigue es determinar el rumbo y la distancia a navegar para unir ambos puntos. Para ello será preciso hacer un cálculo previo utilizando la fórmula de la tangente ya vista al comienzo:
tg R = A / Dj tg R = 3.706’ / 94,2’ (el valor Dj ex-
presado en minutos) tg R = 39,3418259
A partir del valor de la tangente obtenido, sería muy sencillo en este punto determinar el rumbo matemáticamente, obrando como vimos con anterioridad, es decir calculando el arco tangente:
R = arc. tg 39,3418259 R = 88,5o
Veremos cómo se hace lo mismo operando con la tabla:
Una vez obtenido el valor de la tangente del rumbo, se debe buscar la página de las tablas de estima que contenga dicho valor, el cual viene expresado en la parte inferior o superior de cada página. En caso de no encontrar el valor buscado, debe utilizarse el más aproximado. En nuestro caso, el valor más cercano encontrado es tg R = 28,64 al pie de la página que contiene los rumbos 88o, 92o, 268o y 272o (Fig. 102). El valor de “tg R” que sigue aparece tabulado en la página siguiente y es de 57,29. Este último corresponde al rumbo 89o. Como sabemos, en el problema planteado el rumbo pertenece al primer cuadrante, por lo que se debería tomar el rumbo 88o o el 89o, descartando los demás. Dado que el valor de la “tg R” obtenido se encuentra comprendido entre los rumbos 88o y 89o, podemos efectuar una interpolación mental aproximada, determinando así que el rumbo a seguir es de 88,5o.
Para determinar la distancia, en la página correspondiente al rumbo 88o se deberá subir por la columna “E.W.” con el valor del apartamiento y por la columna “N.S.” con el Dj obtenido anteriormente. Aquí nuevamente se nos presenta el mismo problema: el valor del apartamiento supera los máximos tabulados en la tabla. Para resolver el dilema, dividiremos tanto al apartamiento (3.706’) como al Dj (94,2’)
por 20, y multiplicaremos por 20 el resultado obtenido.
A = 3.706 / 20 = 185,3’
Dj = 94,2’ / 20 = 4,71
Ingresamos a la tabla por la parte inferior hasta encontrar en la columna “E.W.” el valor más aproximado a 185,3’, y por la columna “N.S.” el valor más cercano a 4,71’. Como puede comprobarse en la figura No 102, el valor de nuestro apartamiento (185,3’) se encuentra comprendido entre las filas que contienen los valores 184,9’ y 185,9’, dando como resultado distancias de 185 y 186 millas náuticas, respectivamente.
Haciendo una interpolación aproximada entre ambos valores, podemos determinar que la distancia obtenida es de 185,5 millas náuticas. Procederemos a multiplicarlo por 20, tal como habíamos dicho.
D = 185,5 Mn x 20
D = 3.710 Mn.
En realidad, si se piensa detenidamente, el valor de la distancia recorrida en un rumbo de 90o debería ser igual al del apartamiento. En nuestro caso, y dado que el rumbo es muy cercano a 90o, el valor de la distancia resultante debería ser al menos, algo mayor que el del apartamiento, cosa que se cumple a la perfección (D = 3.710 Mn; A = 3.706 Mn).
Hemos determinado, a través de las tablas de estima, el rumbo verdadero al que se debe gobernar para unir a las ciudades de Montevideo y de Ciudad del Cabo, además de la distancia loxodrómica que las separa. Si cotejamos estos datos con los resultados obtenidos empleando las fórmulas matemáticas, al igual que en el caso de la estima directa, comprobaremos que las diferencias no son tantas, teniendo en cuenta los redondeos a que nos obliga el uso de tablas.
Con las fórmulas:
R = 88,5o
D = 3709,6 Mn
Con las tablas de estima:
R = 88,5o
D = 3710 Mn
Habiendo averiguado la distancia loxodrómica, sólo resta determinar la distancia que separa a ambas ciudades navegando por el círculo máximo y cotejar luego las diferencias.
Continua en: La Derrota Ortodrómica: El Triángulo Terrestre (Clase 42)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!