Viene de: Las primeras cartografías (clase 14).
El legado griego
No existen dudas de que los primeros en afirmar y sostener la esfericidad terrestre fueron los griegos, a partir del legado de Pitágoras. Entre ellos, el más grande geógrafo conocido fue Dicearco, nacido en la ciudad de Mesina, quien fue el primero en dimensionar el mundo conocido y habitado (ecúmene), al cual le asignó 40.000 estadios de Norte a Sur y 60.000 de Este a Oeste. En su representación aparece una línea a la que denominó “Diaphragma”, la que atravesando el Mar Mediterráneo, dividía a la superficie terrestre en dos mitades: una septentrional y otra meridional. En el mismo diseño agrega una segunda línea que, pasando por Rodas, dividía al ecúmene en oriente y occidente.
A Dicearco se le atribuyen una enorme cantidad de aportes y descubrimientos, entre otros la medida del arco de meridiano anterior y una minuciosa y detallada descripción general de la tierra.

Según se sabe, Alejandro Magno (discípulo de Aristóteles) fue otro gran estudioso de las cartografías, a sabiendas de que el conocimiento del terreno era por aquel entonces un invalorable instrumento de poder para el gobierno.
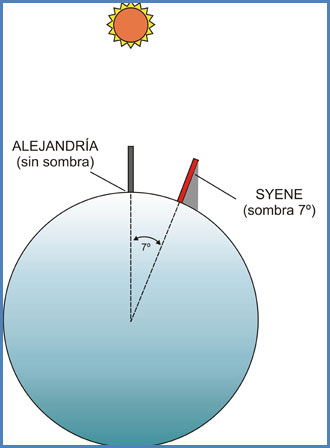
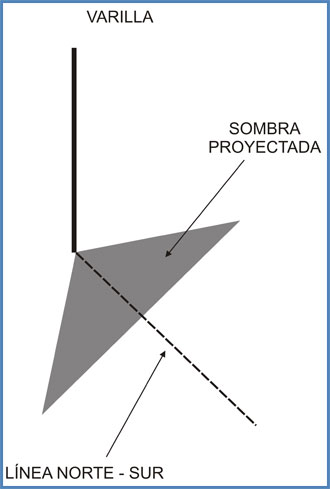
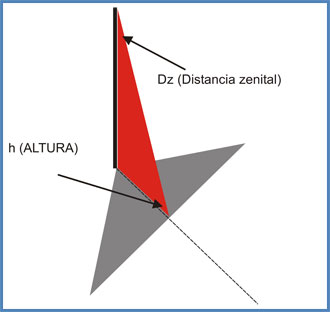
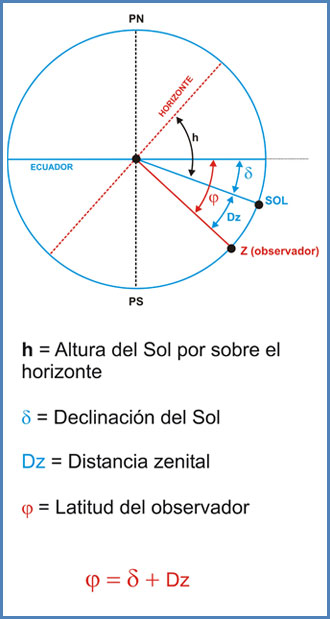
Entre los grandes matemáticos y geómetras de la época no podemos olvidar a Eratóstenes, por ser el primero en calcular (con un error de unos pocos kilómetros) el perímetro terrestre, descubrimiento que le valió su tan merecida fama. El genial Eratóstenes, quien fuera director de la Biblioteca de Alejandría, confeccionó un interesante mapamundi al que le incorporó un entramado de rectas paralelas y perpendiculares entre sí, muy similar al sistema de coordenadas que hoy todos conocemos. De ahí que se le reconozca como el padre del sistema de coordenadas geográficas Latitud y Longitud.

No olvidemos mencionar, entre los griegos, al astrónomo y geógrafo Claudio Ptolomeo. Si bien fue conocido por su célebre “Almagesto” (un colosal tratado de astronomía), se podría decir con justicia que fue el precursor de la cartografía actual. Entre sus logros se cuenta el haber ideado cuatro sistemas diferentes para obtener una cartografía plana y completa del mundo, sistema mediante el cual logró llevar al papel cerca de ocho mil lugares clasificados por regiones, cada cual con sus respectivas coordenadas geográficas. Todo ello fue incluido en los ocho enormes tomos de su “Geografía”. Fue además el primero en hablar de las longitudes.
El Catastro Romano
Si bien el Imperio Romano tuvo también un gran desarrollo topográfico, imprescindible para la construcción de sus colosales obras y acueductos, su aporte más significativo se encuentra en el campo catastral. El levantamiento y posterior representación de cada parcela del terreno en los mapas catastrales era de una precisión sorprendente, y esto tenía un fin concreto: el cobro de impuestos.
De más está decir que el carácter fiscal del catastro romano no agradaba demasiado a la población de aquella época, ya que muchas veces esto traía aparejado el maltrato e incluso la vejación física de los morosos. Por otra parte, el crecimiento de esta práctica trajo acarreado, inevitablemente, el desarrollo de instrumentos de medición muy precisos. Se sabe que los romanos profundizaron sensiblemente el uso de la “Dioptra” (tomada de los griegos), precursora del actual teodolito, utilizado hoy en día por los agrimensores.

Un claro ejemplo de la excelente cartografía romana puede verse en el “Forma Urbis Romae”, del que aún se conservan restos. El gigantesco mapa de 13 metros de altura por 17 metros de ancho, representaba el plano oficial de la ciudad de Roma y se encontraba grabado sobre 151 placas de mármol amuradas sobre una de las paredes de la iglesia de San Cosme.
Continua en: El retroceso medieval (Clase 16)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!