Viene de La declinación magnética (clase 21)
Así como una isobara es una línea que une puntos de igual presión, una isógona es una línea que une puntos de igual declinación magnética (del griego isogonios = iguales ángulos). La cartografía magnética se basa en cartas donde se describen las declinaciones magnéticas de toda la esfera terrestre mediante el trazado de líneas isógonas. Estas cartas reciben el nombre de cartas isogónicas.
El Servicio de Hidrografía Naval de los Estados Unidos publica anualmente planisferios de líneas isógonas, al igual que otros servicios del mundo. Se publican además cartas de zonas polares poco exploradas (por encima del paralelo 70o) Téngase en cuenta que si en latitudes navegables la declinación magnética puede llegar a alcanzar valores cercanos a los 90o, en determinada posición entre los polos magnético y geográfico la declinación puede ser incluso de 180 o (Fig. 59).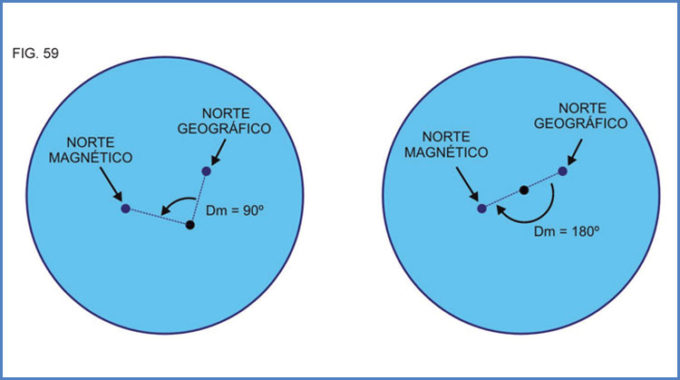
Otro tipo de cartas que brindan información acerca del magnetismo terrestre son aquellas que contienen líneas isóclinas (líneas que unen puntos de igual inclinación). A su vez, hay cartografía donde se describe la intensidad del campo magnético en determinadas regiones. Estas cartas están conformadas por líneas isodinámicas (líneas que unen puntos de igual fuerza magnética).
Aunque en realidad existe una gran cantidad de publicaciones (incluidas las Pilots Charts) donde se pueden obtener los datos de las declinaciones magnéticas, lo usual para los navegantes es recurrir a las cartas náuticas de la zona a navegar. En cartas de pequeña escala, donde suponemos que los valores de declinación magnética se consideran iguales para toda la zona, aparece el dato de la declinación magnética para toda la carta en la “rosa de los vientos” (Fig. 60). Dicho dato contendrá el valor de la declinación para el año de edición de la carta, así como también la “corrección anual” a efectuar.
Ejemplo:
De la rosa de los vientos de la figura se obtiene el valor de la declinación que será 7 36’ W para el año 2008 y el incremento anual será de 8’ al oeste. Si estuviésemos en 2012 tendríamos que multiplicar el valor del incremento anual (8’) por la cantidad de años transcurridos (4). Esto da un incremento total de 32’. Sumamos los 32’ al valor inicial (7o 36’) y obtenemos el valor de la declinación magnética para el año 2012: 8o 8 W’.
En cartas de gran escala que abarcan mayor superficie terrestre, las declinaciones magnéticas no serán las mismas en toda la carta. En este caso las declinaciones se grafican con líneas isógonas paralelas entre sí.
Continua en: Cálculo del Rumbo Verdadero a partir del Norte Magnético y el desvío del compás (Clase 23)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestros teléfonos 4383-3843/4395, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!