Viene de: La Proyección Cilíndrica (clase 10).

La mercatoriana es una proyección perteneciente al grupo de las modificadas y es una derivada de las cilíndricas. El célebre cartógrafo partió de la proyección cilíndrica centrográfica y la modificó sustancialmente. La base principal de dicha modificación se basa en que reemplazó al único cilindro por una serie infinita de ellos, cada uno de los cuales es tangente a lo largo de toda la superficie terrestre. Cada uno de los cilindros de la proyección mercatoriana, una vez desarrollados, solo tiene en cuenta el crecimiento de la escala de las latitudes, mientras que la separación de los meridianos se mantiene constante e idéntica a la correspondiente al cilindro tangente en el Ecuador.

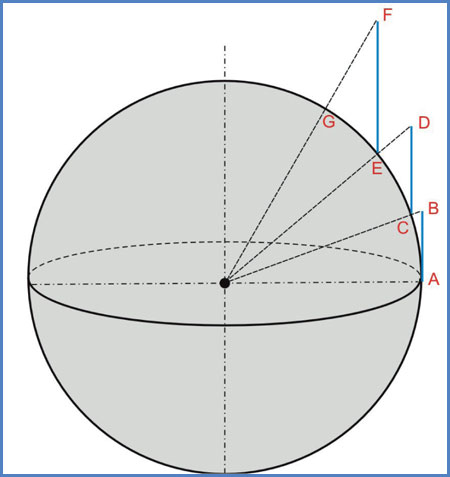
Los triángulos ABC (considerado recto en C), CDE (considerado recto en E) y EFG (considerado recto en G) son el resultado de proyectar, desde el centro de la esfera, los puntos C, E y G sobre distintos cilindros, cada uno de los cuales es tangente a los puntos proyectados. Una vez sumados los distintos trozos de proyección se obtendrá una carta cuya representación gráfica es también conocida como “latitudes aumentadas”.

La fórmula matemática que resultó sería la base de la proyección mercatoriana y se utilizó por primera vez en una carta publicada en Duisburgo en el año 1569. Por ese entonces no se conocía con precisión el radio terrestre, por lo que dicha fórmula era válida solamente para una Tierra esférica. Por esa razón se consideró a dicha proyección dentro del tipo de las esféricas. Esto traía acarreadas algunas imprecisiones, las que fueron resueltas algunos años después, cuando la ciencia permitió conocer con exactitud el radio en los diferentes puntos de la Tierra. A partir de entonces fue introducido en la fórmula original un factor de corrección, a fin de suprimir los inconvenientes antes mencionados.

Dependiendo de la posición que ocupe el cilindro que se circunscribe a la esfera terrestre, la proyección resultante puede recibir diferentes denominaciones.

La mercatoriana vista con anterioridad, en la que el cilindro es tangente en el Ecuador, recibe el nombre de “proyección mercatoriana directa”. Esta es, sin lugar a dudas, la más empleada de todas las proyecciones. Cuando el cilindro es tangente a cualquier otro círculo máximo, recibe el nombre de “transversa”. Aquí puede darse el caso de que la tangencia sea con un meridiano cualquiera, proyección que llevará el nombre de “mercatoriana inversa”, o bien que la tangencia sea con cualquier otro círculo máximo. En este último caso la resultante recibirá el nombre de “proyección mercatoriana oblicua”.

La proyección mercatoriana inversa es útil cuando lo que se desea representar es una zona comprendida entre los polos, sin abarcar demasiada extensión en longitud. Pueden ser utilizadas también en navegaciones cercanas a cualquiera de los polos. En estos casos (latitudes altas) los meridianos presentarán una ligera curvatura, mientras que los paralelos se asemejarán a círculos.

Dentro de las proyecciones modificadas, la otra proyección muy utilizada es la azimutal equidistante, derivada de las proyecciones estereográficas. Dentro de esta categoría podemos encontrar las tres clases de gnomónicas vistas con anterioridad: polar, meridiana y horizontal, dependiendo de la posición del plano de tangencia.

La más común de todas es la carta con proyección azimutal equidistante polar, cuya ventaja fundamental reside en que en una sola carta puede representarse todo el globo terráqueo.

En este tipo de proyección, los meridianos serán rectas concurrentes que convergerán en los polos, mientras que los paralelos serán círculos concéntricos separados, de manera tal de conservar sus distancias reales en la Tierra. De este modo, los círculos que representan a cada uno de los paralelos serán equidistantes entre sí, lo que da origen a la denominación de la proyección. La dificultad de este tipo de proyección es que sufre grandes deformaciones en la cercanía de los polos, tanto en ángulos como en distancia. Esta es en realidad una proyección calculada, ya que no surge geométricamente sino a partir de formulaciones matemáticas. Este tipo de proyección es utilizada, por ejemplo, en la representación de la esfera celeste que utiliza el identificador de estrellas conocido como “Star Finder No 2102”, o cualquier otro mapa celeste.

Continua en: Proyecciones Modificadas (clase 11)

Darío G. Fernández
Director del ISNDF

Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!