Viene de La Derrota Ortodrómica: El Triángulo Terrestre (Clase 42)
A fin de ejemplificar el cálculo retomaremos la navegación planteada anteriormente y la calcularemos navegando por el círculo máximo.
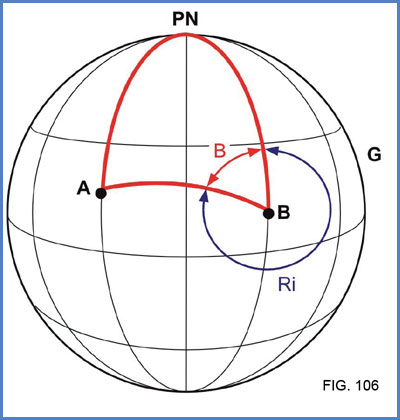
El primer paso antes de aplicar las fórmulas vistas es calcular la diferencia en longitud entre ambos puntos (fig. 107):
Dw = w1 + w2 Dw = 56o 7,6’ + 18o 25,6’ Dw = 74o 33,2’
Hecho esto, calcularemos en primer término la distancia que separa ambos puntos aplicando para ello la fórmula del coseno:
cos (A – B) = sen jA x sen jB + cos jA x cos jB x cos Dw
Reemplazando en ella los valores:
cos (A-B) = sen (-34o 54,5’) x sen (-33o 20,3’) + cos (-34o 54,5’) x cos (-33o 20,3’) x cos (74o 33,2’)
cos (A-B) = (-0,572265) x (-0,549581) + (0,820068) x (0,835439) x (0,266341)
cos (A-B) = 0,314505 + 0,182474 cos (A-B) = 0,496979 D = arc cos 0,496979 D = 60,19o
En millas náuticas: D = 60,19o x 60’ = 3.611 D = 3.611 Mn
Para determinar el rumbo inicial al que se debe navegar, aplicaremos la fórmula de la cotangente:
cotg Ri = (cos jA x tg jB – sen jA x cos Dw) / sen Dw
cotg Ri = [ cos (-34o 54,5’) x tg (-33o 20,3’) – sen (-34o 54,5’) x cos (74o 33,2’) ] / sen (74o 33,2’)
cotg Ri = [ (0,820068) x (-0,657835) – (-0,572265) x (0,266341) ] / 0,963878
cotg Ri = [ (-0,539469) – (-0,152441) ] / 0,963878
cotg Ri = -0,387028 / 0,963878 cotg Ri = -0,401532 Ri = arc cotg (-0,401532) Ri = 112o
Hemos arribado al resultado esperado: el rumbo inicial a navegar por la ortodromia, es decir por la ruta mas corta.
Un concepto de interés: Como puede comprobarse en el esquema de la figura 107, el valor obtenido no corresponde al ángulo interior con vértice en “A” del triángulo terrestre conformado con el Polo Sur, sino que es su suplemento, es decir el que le corresponde al triángulo conformado con el Polo Norte (ángulo “Ri”). Por esa razón, el ángulo obtenido es directamente el Rumbo inicial. Esto habitualmente ocurre así, salvo para algunos valores de seno y coseno muy cercanos a 0 ó a 1, en cuyo caso el ángulo resultante podría ser el opuesto (ángulo “A” en la figura). De haber ocurrido así, es decir que el valor obtenido hubiese correspondido al del ángulo “A”, el procedimiento a seguir sería restar dicho valor a 180o (Ri = 180o – A), por ser ambos ángulos (“A” y “Ri”) suplementarios entre sí. Esto es producto de cuestiones de la trigonometría que, por razones de espacio, no se tratarán en este apartado. En cualquier caso y para facilitar al lector la tarea, sugerimos dibujar un esquema a mano alzada a fin de determinar en forma gráfica a cuál de los dos ángulos corresponde el valor obtenido en el cálculo. En el caso aquí planteado resulta sencillo ya que, como se aprecia claramente en el esquema de la figura No 107, el ángulo “Ri” es mayor a 90o, mientras que su suplemento (“A”) es menor a 90o. Por lo tanto, el resultado obtenido (112o) sólo puede corresponder al triángulo con vértice en el Polo Norte.

Un cálculo adicional de interés para el navegante cuando se plantea una navegación ortodrómica, es el de las coordenadas del punto donde la derrota alcanza la máxima latitud. A este punto se lo denomina “Vértice de la ortodromia”. Este dato puede ser de utilidad en el caso de que no se desee sobrepasar determinada latitud en función de las condiciones meteorológicas posibles. La coordenada latitud del “Vértice” (jV) se puede establecer aplicando la fórmula:
cos jV = cos jA x sen Ri
Para obtener la longitud del “Vértice” es preciso calcular en primer lugar la diferencia en longitud (Dw) que existe entre la longitud de salida (wA) y la longitud del vértice (wV), lo que puede resolverse con la fórmula:
cotg Dw = sen jA x tg Ri
Una vez obtenido el Dw, se calcula la coordenada longitud del vértice simplemente sumando o restando dicho Dw a la longitud de salida wA:
wV = wA +/- Dw
Habiendo finalizado con el análisis de una derrota ortodrómica, compararemos los resultados obtenidos con los de la derrota loxodrómica obtenidos al comienzo:
Por la loxodromia:
R = 88,5o D = 3709,6 Mn
Por la ortodromia:
Ri = 112o D = 3611 Mn
Como puede verse, la derrota loxodrómica implica navegar casi 100 millas de más, pero siempre a rumbo 88,5o. Como contrapartida, la ortodromia pretende una distancia menor, pero zarpando a rumbo inicial 112o y modificando el mismo cada 200 ó 300 millas náuticas.
Continua en: La navegación costera: Linea de posición (Clase 44)
Darío G. Fernández
Director del ISNDF
Si desea realizar el curso de patrón de yate completo en nuestro instituto, puede contactarse con nosotros a través de nuestro teléfono Cel. (011) 15 5644-2888, o bien vía mail a secretaria@isndf.com.ar
Aprenda a navegar con nosotros, lo llevaremos a buen puerto!



